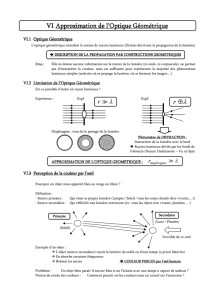
1 Introduction à la Théorie géométrique de la diffraction

Introduction à la Théorie géométrique de la diffraction –Présentation JWAYA 2011 1
Introduction à la Théorie
géométrique de la diffraction
Professeur Patrick VAUDON
Université de Limoges - France

Introduction à la Théorie géométrique de la diffraction –Présentation JWAYA 2011 2
Théorie géométrique de la diffraction
Définition : Méthode de calcul dite asymptotique,
c’est à dire d’autant plus exacte que la fréquence est
plus élevée.
Concrètement : il s’agit de méthodes de calcul du
champ électromagnétique, intermédiaires entre les
méthodes à formulation rigoureuses et les méthodes
optiques.

Introduction à la Théorie géométrique de la diffraction –Présentation JWAYA 2011 3
Les besoins de calculs du champ
électromagnétique
-Diagramme de rayonnement des antennes.
- Analyse du canal de propagation.
- Calculs de surface équivalente radar.
- Calculs des niveaux des parasites
électromagnétiques (compatibilité EM)
-IEMN, MPF, guerre électronique, etc …..

Introduction à la Théorie géométrique de la diffraction –Présentation JWAYA 2011 4
Les méthodes de calcul du champ
électromagnétique
-Les méthodes exactes (Solutions exactes des équations de
MAXWELL) (Solutions peu nombreuses)
- Les méthodes rigoureuses à formulation numérique (Discrétisation des
équations de MAXWELL) (Volume de calcul limité)
- Les méthodes asymptotiques (TGD, Optique physique) (Méthodes
approchées)
Ce sont les seules méthodes utilisables pour traiter des objets dont les
dimensions sont grandes devant la longueur d’onde.

Introduction à la Théorie géométrique de la diffraction –Présentation JWAYA 2011 5
Exemple de calcul avec un dipôle
-Dipôle : fil dont la longueur est très inférieure à la longueur d’onde
- Diagramme de rayonnement en espace libre :
F() = |sin()| avec une symétrie de révolution autour du fil
- Champ électrique rayonné à grande distance :
 U
r
e
sinEE jkr
0