Angle inscrit_au centre

CERCLES - ANGLES INSCRITS - ANGLES AU CENTRE
1. Définitions
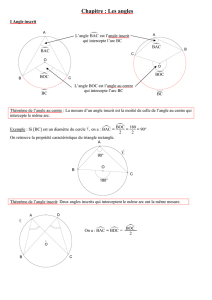
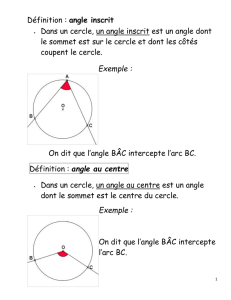
A) Angle au centre
Un angle au centre est un angle dont le sommet est le centre du cercle.
BOC est un angle au centre.
BOC intercepte l’arc AB
B) Angle inscrit
Un angle inscrit est un angle dont le sommet est sur le cercle et dont les côtés sont sécants
avec le cercle.
non non oui oui
L’angle inscrit BAC intercepte l’arc BC
2. Propriété
A) Exemple
L’angle inscrit BAC et l’angle au centre BOC
interceptent le même arc de cercle BC.
D’après les mesures indiquées, on a :
BAC = 20° + 40°
BAC = 60°
Nous allons montrer que BOC = 120°
B
OC
B
OC
B
OC
C
O
A
B
CO
A
B
C
O
A
B
O
A
B
C
O
A
B
C
B
OC
20°40°
?
12
O
A
B
C
B
OC
B
OC
B
OC
B
OC
B
OC

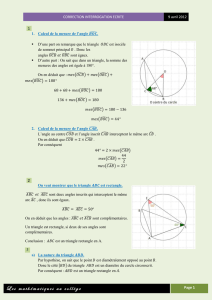
Un tour complet autour du point O correspond à un angle de 360°. Donc
BOC = 360° – ( O1 + O2 ) égalité ➀
Le triangle BOA est isocèle en O. Ses angles à la base sont égaux. Par suite, on a :
O1 = 180° – 2 x 20°
= 180° – 40°
= 140°
Le triangle COA est isocèle en O. Ses angles à la base sont égaux. Par suite, on a :
O2 = 180° – 2 x 40°
= 180° – 80°
= 100°
L’égalité ➀ devient :
BOC = 306° – ( 140° + 100° )
= 360° – 240°
= 120° CQFD
B) Théorème
SI, dans un cercle, un angle au centre et un angle inscrit interceptent le même arc,
ALORS l’angle au centre vaut le double de l’angle inscrit.
C) Démonstration
Raisonnons comme pour l’exemple.
BOC = 360° – ( O1 + O2 ) égalité ➀
Dans le triangle BOA isocèle en O, on a :
O1 = 180° – 2 x A1
= 180° – 2 A1
Dans le triangle COA isocèle en 0, on a :
O2 = 180° – 2 x A2
= 180° – 2 A2
L’égalité ➀ devient :
BOC = 360° – [ ( 180° – 2 A1 ) + ( 180° – 2 A2 ) ]
= 360° – [ 360° – 2 A1 – 2 A2 ]
= 360° – 360° + 2 A1 + 2 A2
= 2 ( A1 + A2 )
Or, d’après la disposition
A
1 + A2 = BAC
Donc BOC = 2 x BAC CQFD
12
O
A
B
C
12
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC
B
OC

3. Angles inscrits égaux
BIC et BJC sont deux angles inscrits qui interceptent le même arc BC.
Donc, ils ont égaux chacun à la moitié de l’angle au centre BOC.
Par suite, ils sont égaux : BIC = BJC
Théorème
SI deux angles inscrits interceptent le même arc de cercle ALORS ils sont égaux.
O
B
C
I
J
B
OC
B
OC
B
OC
B
OC
B
OC