Raisonnement par disjonction des cas

2014-2015 Logique
Raisonnement par disjonction des cas
Soit P et Q deux propositions.
Pour montrer que « P ⇒Q » , on sépare l’hypothèse P de départ en différents
cas possibles et on montre que l’implication est vraie dans chacun des cas.
Exemple 1
On montre, par disjonction des cas, la proposition : « Pour tout entier n,n(n+ 1)
2est un entier. »
Cette proposition se formule aussi de la façon suivante : « Si n∈Z, alors n(n+ 1)
2∈Z. »
Soit nun entier. Il y a deux cas possibles : nest pair ou nest impair.
Premier cas :nest pair.
Alors il existe un entier ktel que n= 2ket n(n+ 1)
2=k(2k+ 1) donc n(n+ 1) 2est un entier.
Deuxième cas :nest impair.
Alors il existe un entier ktel que n= 2k+ 1 et n(n+ 1)
2= (2k+ 1)(k+ 1) donc n(n+ 1) 2est
un entier.
On a bien montré que, pour tout entier n,n(n+ 1)
2est un entier.
Exemple 2
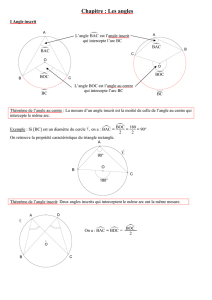
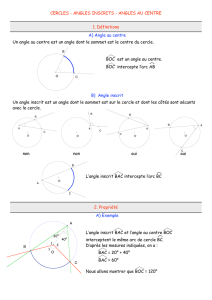
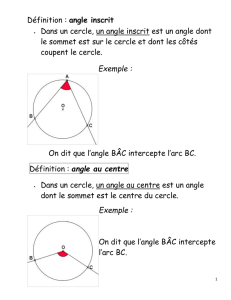
Théorème de l’angle inscrit :
Dans tout cercle, tout angle inscrit est égal à la moitié de l’angle au centre qui intercepte le
même arc que l’angle inscrit.
Pour démontrer ce théorème, on considère trois cas, selon la position du centre du cercle par
rapport aux côtés de l’angle inscrit :
Premier cas : le centre est situé sur un des côtés de l’angle inscrit.
O
AB
C
Le triangle AOC est un triangle isocèle en Odonc [ OAC =[ OCA.
La somme des angles d’un triangle vaut 180˚donc [ AOC = 180˚−[ OAC −[ OCA = 180˚−2[ OAC.
Les points A,Oet Csont alignés donc \ BOC = 180˚−[ AOC .
On a alors : \ BOC = 180˚−(180˚−2[ OAC ) = 2 [ OAC .
1

2014-2015 Logique
Comme les points A,Oet Csont alignés, on a [ OAC =\ BAC .
On en conclut : \ BOC = 2 [ AOC .
Deuxième cas : le centre est situé à l’intérieur de l’angle inscrit.
O
AD
C
B
On construit le point Ddiamétralement opposé à Asur le cercle.
\
BOC =\ BOD +\ DOC .
D’après le premier cas de figure, \ BOD = 2\ BAD et \ DOC = 2\ DAC.
On a alors \ BOC = 2\ BAD + 2\ DAC = 2(\ BAD +\ DAC) = 2\ BAC.
Troisième cas : le centre est situé à l’extérieur de l’angle inscrit.
O
AD
C
B
On construit le point Ddiamétralement opposé à Asur le cercle.
\
BOC =\ DOC −\ DOB.
D’après le premier cas de figure, \ DOC = 2\ DAC et \ DOB = 2\ DAB.
On a alors \ BOC = 2\ DAC −2\ DAB = 2(\ DAC −\ DAB) = 2\ BAC.
2