Initiation aux statistiques inférentielles

1
Initiation aux statistiques inférentielles
•Chapitre 1 : les échantillons
•Chapitre 2 : la loi normale : première loi
d’échantillonnage
•Chapitre 3 : l’estimation ponctuelle et par
intervalle de confiance
•Chapitre 4 : l’initiation aux tests d’hypothèse

2
INTRODUCTION
A. Les indicateurs des
échantillons
1°) Exemple 1.
2°) Exemple 2.
3°) Exemple 3.
B. Les fluctuations d’échantillonage.
1°) Objectif .
2°) Exemple.
C. Les sondages classiques
1°) Les sondages aléatoires.
2°) les sondages empiriques.
Mises en garde.
CHAPITRE 1 : LES ECHANTILLONS

3
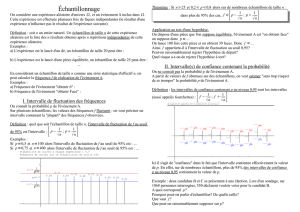
Si dans un échantillon de 1 000 personnes, 200 votent pour A alors est-on vraiment certain que A
réalisera un score de 20 % lors de l’ élection ?
Par exemple, si le poids moyen des paquets de la production est de 250 grammes, il est
possible de trouver un échantillon de poids moyen 249 grammes
•Le comportement des échantillons est incertain :
•Troisième objectif : comparer deux (ou plus) traitements différents : en ressources humaines, peut-on
affirmer que depuis la création de la crèche d’ entreprise, le taux d’ absentéisme a baissé ; en marketing,
les ventes réalisées sont-elles différentes avec ce nouvel emballage ?
•Deuxième objectif : Vérifier si la production est conforme aux attentes ou spécifications.
•Premier objectif : Connaître les propriétés de la population dont est extrait l’ échantillon.
Les objectifs
CHAPITRE 1 : LES ECHANTILLONS

4
Incertain et Aléatoire
•Par exemple, si le poids moyen des paquets de la production est de 250 grammes, il est possible de
trouver un échantillon de poids moyen 249 grammes mais avec quelle probabilité ?
•Autre exemple : si dans un échantillon de 1 000 personnes, 200 votent pour A alors est-on vraiment
certain que A réalisera un score de 20 % lors de l’ élection ? Avec quelle certitude ?
entre 19 % et 21 % ?
•On peut penser que, si le sondage est bien fait, A réalisera un score «autour» de 20 % mais la
question devient alors :
entre 17 % et 23 % ?
entre 10 % et 30 % ?
«il va peut-être pleuvoir» et «il y a une probabilité de 30 % qu’il pleuve»
Si je connais cette probabilité, j’adapte mon comportement et je prends ou pas mon parapluie
CHAPITRE 1 : LES ECHANTILLONS

5
•Parmi ces trois échantillons qui suivent, y en a-t-il qui sont manifestement
gaussiens ?
•L’utilisation de la loi normale dont la caractéristique principale est sa
forme de «courbe en cloche» est fondamentale
Echantillon Gaussien
CHAPITRE 1 : LES ECHANTILLONS