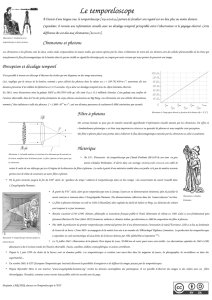
Déviation de la lumière

On constate que l’étoile ne parait pas à la même
position après que la Terre ait effectué une demi-
révolution autour du Soleil
PROBLEMATIQUE :
En observant une étoile située près du soleil,
on a noté 2 fois sa position !

Question :
Comment se fait-il que l’étoile n’ait pas à la
même position lors des deux observations, ou
que l’on observe quatre fois la même galaxie ?
Hypothèse :
On peut supposer que la lumière est déviée par
la présence du Soleil ou d’un autre astre.
On remarque aussi des galaxies qui se voient en quadruple !

1.Protocole
Pour représenter la déviation de la lumière, on peut
ramener l’univers en quatre dimensions à seulement deux.
Pour cela on pourra le représenter à l’aide d’une nappe
tendue sur un plan en deux dimensions.
Les photons peuvent être assimilés à des billes se
déplaçant sur cette nappe.
Un corps massif pourra être représenté par un ballon.
Vérification expérimentale

2. Matériel
Le montage que nous vous proposons est une nappe
tendue à l’aide de fixations aux quatre coins et un ballon
au centre. Les photons seront des billes de plomb.