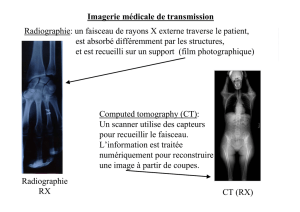
Exercice 1 : Interactions des photons avec la matière ( 13 pts )

 Célérité de la lumière dans le vide : C = 3,0.108 m.s-1
 Charge électrique élémentaire : e = 1,6.10-19 C
 Constante de PLANCK : h = 6,62.10-34 J.s
 Unités de masse : 1 u = 1,66054. 10-27 kg = 931,5 MeV.C-2
 Masses des particules : électron –me= 5,48.10-4 u
Exercice 1 : Interactions des photons avec la matière ( 13 pts )
D’après le DTS IMRT de juin 2008
L'énergie de liaison d'un électron situé sur la couche K d'un atome de
plomb est de 88 keV.
1 - Effet photoélectrique
1-1 Donner la définition de l'effet photoélectrique. Décrire brièvement ce phénomène.
1-2 On envoie un photon d'énergie 90 keV sur du plomb. Quelle est l'énergie cinétique de l'électron
émis par effet photoélectrique ? Quelle est sa vitesse ?
2. Effet Compton
Un photon d'énergie E = 660 keV interagit par effet Compton avec un électron. Il projette cet électron
en lui communiquant une énergie cinétique Ec de 97 keV, le reste de l'énergie étant emporté par un photon
diffusé d'énergie E' faisant un angle  avec la direction du photon incident.
2-1 Quelle relation existe-t-il entre E, E' et Ec ? En déduire la valeur de E'.
2-2 Calculer les longueurs d'onde et ' des rayonnements incident et diffusé
2-3 Déduire de la relation de Compton-Debye :
' (1 cos )
.
o
h
mC
la valeur de cos , puis de
 en degrés.
2-4 Le choc était-il frontal ?
3. Matérialisation
3-1 Donner la définition de la matérialisation. Décrire brièvement ce phénomène
3-2 Quelle énergie minimale doit avoir le photon ? Donner le résultat en MeV.
EXERCICE 2 : Atténuation d'un faisceau polyénergétique de photons (7 pts)
D’après le DTS IMRT de juin 2006 ( question 4 indépendante de 1, 2 et 3 )
Un faisceau incident et parallèle de No photons est constitué pour moitié de N1o photons d'énergie
E1=100 keV et pour moitié de N2o photons d'énergie E1=50 keV.
Ce faisceau traverse une plaque de cuivre dont les coefficients d'atténuation linéique sont :
1
10,357mm
pour les photons d'énergie E1
1
22,30mm
pour les photons d'énergie E2
Après la traversée d'une épaisseur x de cuivre, il reste N1 et N2 photons d'énergies respectives El et E2.
On appelle N le nombre total de photons.
l. Calculer les couches de demi-atténuation du cuivre (CDA) pour les photons d'énergie El et E2.
2. Exprimer N1 et N2 en fonction de N1o , N2o, x et des coefficients d'atténuation (
1
et
2
). En déduire
l’expression de N1 et N2 puis de N ( nombre total de photons ) en fonction de No, x et des coefficients
d'atténuation (
1
et
2
).
3. Calculer le pourcentage total de photons restants après traversée de 1,5 mm de cuivre
4. On considère un faisceau monocinétique d'énergie E = 100 keV, calculer l'épaisseur de la plaque de
cuivre qui arrête 30% du rayonnement.
IMRT2 - 2008-2009 Evaluation n°1 15/10/2008