1 et 2 lois de Newton

TP P9
1
ère
et 2
ème
lois de Newton
CORRECTION
1. Vérification du principe de l’inertie (première loi de Newton) : TPP5 1
ère
S
1.1.1. v =
v ²
x
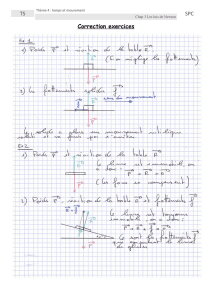
1.1.2. Système : chariot Référentiel : sol (référentiel terrestre considéré galiléen)
Dans les deux cas, la trajectoire du chariot est une droite : le mouvement est rectiligne.
Cas n°1 : La vitesse du chariot ne varie pas : le mouvement est uniforme.
Cas n°2 : La vitesse diminue au cours du temps : le mouvement est ralenti.
1.2. Étude théorique :
1.2.1. Cas n°1 : D’après le principe d’inertie (1
ère
loi de Newton), le mouvement étant rectiligne et
uniforme ( v
G
Cte
= ) alors les forces exercées sur le chariot se compensent. Soit
.
0
ext
F
Σ =
.
Cas n°2 : Le mouvement n’est pas rectiligne uniforme ( v
G
Cte
≠ ) alors d’après le principe d’inertie
.
0
ext
F
Σ ≠
.
1.2.2. Cas n°1 : Le système subit : - son poids
P
- la poussée de l’air
F
Ces forces se compensent.
Cas n°2 : Le système subit : - son poids
P
- la poussée de l’air
F
- la force de frottement du banc
f
: Cette force horizontale, de sens
opposé au sens du mouvement n’est pas compensée par d’autres forces. (Cette force apparaît sur certains
bancs, pour lesquels l’horizontalité n’a pas été effectuée correctement, ou dont la soufflerie est moins
puissante.)
2. Du vecteur variation de vitesse
v
∆
au vecteur accélération
a
:
2.1.Expérience : Système : mobile autoporteur Référentiel : table
2.1.1. La trajectoire est un arc de cercle : le mouvement est circulaire.
Pendant une même durée τ, le mobile parcourt toujours la même distance, la vitesse est constante : le
mouvement est uniforme.
2.2. Vecteur vitesse :
v
2.2.1. v
1
=
0 2
2
G G
τ
=
0 2
2
G G
τ
v
3
=
2 4
2
G G
τ
=
2 4
2
G G
τ
v
1
=
2
3
5,9 10
2 40 10
−
−
×
× ×
= 0,74 m.s
-1
v
3
= v
1
= 0,74 m.s
-1
2.2.2. Les vecteurs
1
v
et
3
v
sont représentés par des flèches de longueur
0,74
0,10
= 7,4 cm
Sens : celui du mouvement
Direction : tangente à la trajectoire en G
i
(donc perpendiculaire au rayon OG)
1
v
G
2
G
3
G
4
G
5
3
v
1
v
−
3
v
2
v
∆
2
a

2.3.1. Détermination du vecteur variation de vitesse
2
∆v
:
2.3.1.1. Construction
2
3 1
∆v = v - v
: voir figure précédente.
2.3.1.2. On mesure à la règle ∆v
2
 2,2 cm donc ∆v
2
= 2,2×0,10 = 0,22 m.s
-1
2.3.2. Détermination du vecteur accélération :
2.3.2.1. a
2
=
2
∆v
∆t
=
2
∆v
2
τ
a
2
=
3
0,22
2 40 10
−
× × = 2,75 = 2,8 m.s
-2
2.3.2.2. Représentation
2
a
:
2,75
0,50
5,5 cm
2.3.2.3. Le vecteur accélération
2
a
est porté par le rayon OG
2
.
2.3.3. Vecteur somme des forces extérieures
.
ext
F
Σ et vecteur accélération
a
:
2.3.3.1. Inventaire des forces subies par le mobile autoporteur :
-
P
poids
-
F
poussée de l’air expulsé par le mobile
-
T
tension du fil
2.3.3.2. Le mobile autoporteur est immobile verticalement, d’après le principe d’inertie les forces
verticales
P
et
F
se compensent soit
P
+
F
=
0
.
On a
.
ext
F
Σ =
T
.
2.3.3.3. On constate que
.
ext
F
Σ a même sens et même direction que le vecteur accélération
a
.
Donc
.
ext
F
Σ = k.
a
2.3.4. Cas particulier du mouvement circulaire uniforme :
2.3.4.1. Le mouvement étant uniforme v
2
= v
1
= v
3
, donc
2
2
v
R
=
0,74²
0,205
= 2,7 m.s
-2
a
2
= 2,8 m.s
-2
Conclusion : dans le cas d’un mouvement circulaire uniforme a
2
=
2
v
R
2.3.4.2. Analyse dimensionnelle : a s’exprime en m.s
-2
alors [a] = [L].[T]
-2
[v] = [L].[T]
-1
[v²] = [L]².[T]
-2
et [R] = [L]
alors
2
v
R
= [L].[T]
-2
, on vérifie que
2
v
R
est homogène à une accélération.
P
F
T

3. Deuxième loi de Newton : « version TS »
3.1. Dispositif expérimental :
3.1.1. Inventaire des forces subies par le mobile : idem 2.3.3.1.
-
P
poids
-
F
poussée de l’air expulsé par le mobile
-
T
tension du fil
3.1.2. On a
.
ext
F
Σ =
T
. (idem 2.3.3.2.)
3.2. Acquisition des positions successives du mobile autoporteur :
3.3. Détermination de la vitesse du mobile : 3.3.1. La courbe représentative
de v
x
= f(t) est une droite (selon
les cas, elle passe ou non par
l’origine).
La coordonnée v
x
augmente au
cours du temps.
3.3.2. La trajectoire du mobile
est une droite ; la vitesse
augmente : le mouvement est
rectiligne et accéléré.
3.4. Détermination de l’accélération du mobile :
3.4.1. a
x
=
x
v
t
d
dt
est égale au coefficient directeur, à la date t, de la tangente à la courbe représentative de
v
x
= f(t).
3.4.2.1. On modélise avec le modèle v
x
= a.t + b. On obtient a = 2,495 m/s/s.
3.4.2.2. Valeur de la coordonnée a
x
du vecteur accélération a
x
= 2,5 m.s
-2
.
Cette valeur est constante au cours du mouvement, en effet le coefficient directeur de la tangente reste le
même quel que soit t.
3.4.2.3. a =
2
x
a
= 2,5 m.s
-2
3.5. Deuxième loi de Newton
3.5.1. m.a = 0,215× 2,5 = 0,54 kg.m.s
-2
.
F T
ext
Σ = = T = 0,5 N
On constate que
.
F
ext
Σ = T = m.a
3.5.2.
.
F
ext
Σ et
a
ont même sens et même direction. De plus
.
F
ext
Σ = m.a.
Alors
.
F
ext
Σ = m.
a
. deuxième loi de Newton. (appelée aussi principe fondamental de la dynamique)
3.5.3.
masse du mobile
(kg) valeur de l’accélération (m.s
-2
) m.a (kg.m.s
-2
) valeur de la tension (N)
0,215 2,5 0,54 0,5
0,215 1,5 0,32 0,3
0,315 1,7 0,54 0,5
0,215 3,2 0,69 0,7
P
F
T