Ts t4ch3 correction ex lois de newton

TS Thème 4 : temps et mouvement SPC
Chap 3 Les lois de Newton
Correction exercices

Ex3 Saut en parachute
1. Le mouvement est rectiligne uniforme si le vecteur vitesse est un vecteur constant :
Le mouvement est étudié dans le référentiel terrestre considéré galiléen.
2. Les actions mécaniques qui s’exercent sur le système constitué par le parachutiste et son parachute sont
les frottement de l'air
⃗
F
et le poids
⃗
P
3. D’après le principe d’inertie, le mouvement étant rectiligne uniforme, on a:
Le poids
⃗
P
est une force verticale dirigée vers le bas, de valeur P = mg ;
La force
⃗
F
est une force verticale dirigée vers le haut, de valeur F = P ; F = 8,8.102 N.
4. La distance parcourue est d= 400 m et la durée est Δt = 1min 30s = 90s.
La vitesse du parachutiste est
Ex4 Détermination des caractéristiques d'une force

Ex 5 Caractériser les force et le mouvement
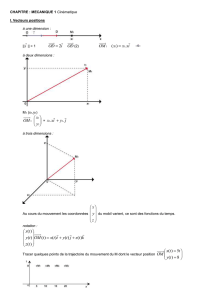
Le vecteur vitesse
⃗
v
a le sens du déplacement, le sens du vecteur accélération
⃗
a
dépend de la nature accélérée ou
décélérée du mouvement. Le vecteur représentant la force
⃗
F
qui s’exerce sur le point matériel est lié au vecteur accélération
⃗
F
par la deuxième loi de Newton avec m masse du point matériel. Le vecteur
⃗
F
a donc le même sens que
⃗
a
Enregistrement 1 : mouvement rectiligne décéléré, les vecteurs
⃗
a
et
⃗
v
sont de sens opposés.
Enregistrement 2 : mouvement rectiligne uniforme,
Enregistrement 3 : mouvement rectiligne accéléré, les vecteurs
⃗
a
et
⃗
v
ont même sens.

Ex6 Caractériser une accélération lors d'un saut
1. Le parachutiste équipé est le système choisi.
Les forces qui s’exercent sur le système sont : son poids de valeur P = 800 N et la force due à l’air.
En appliquant la deuxième loi de Newton au système dont la masse est constante :
En projetant cette relation sur un axe vertical, on trouve P - Fair = m.a
Le vecteur accélération est vertical, dirigé vers le bas et sa valeur est
Par exemple, pour le cas 2
a=(80×10)−350
80 =5,6 m.s−1
2.
1