La dur ée At, l`intervalle de temps qui sépare deux _d

L'essentiel
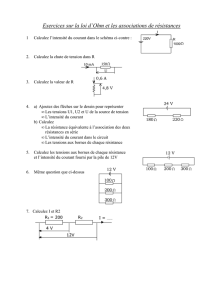
La vitesse moyenne est le quotient de la distance
parcourue par la durée du parcours :
U-o,
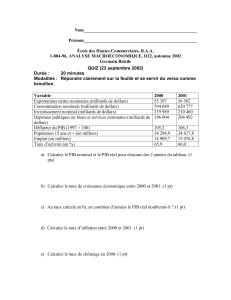
La dur ée At, l'intervalle de temps qui sépare deux
événements, s'obtient en soustrayant les instants
auxquels ils se produisent.
La trajectoire d'un point matériel est I'ensemble des
positions occupées par ce point au cours du temps.
La position initiale (finale) est la position occupée
par le point mobile à I'instant initial (final).
_d
Lt
Les exercices qu'il faut pouvoir faire
Rappels
o (Jne hetre contplc 60 ntinnle.r, /tn( ntintte conple
1600.ç dan.r rrnt Lterrrt. I/-7, a 21 lt dan.ç unjrtur.
o Las abÉriatiott.r ]totr u lilit:ltfu " el ç ,rt,;62fl1' ', (de
< .ç >. Ainsi, / rttinrrte 12 .çecondes 950 rti//iàne'ç.çe
60 .ceconde.r... I/-1, a drtnc
TEMP! .îon/ ,, trtitt ,, el
notc :
/ ttin 12,950 .ç
(el pa.r l'12,950" cltti corre.rl>ond r) un AII{GLE).
1. Convertissez les vitesses suivantes en m,/s :
72kmlh,5 km/h (vitesse d'un marcheur), 30 km/s (vitesse
de la Terre autour du Soleil).
2. Convertissez en km/ln :
10 m/s (vitesse moyenne d'un sprinter), 330 m/s (vitesse du
son dans I'air).
3. Un athlète court un marathon (42,195 km) en 2 h 5 min 42 s.
Calculez sa vitesse moyenne.
4. Je pars de la maison à 8 h 20 min 30 s. Le compteur de ma
voiture indique 437,2 km. Je me gare près du bureau à t h
2 min 40 s. Le compteur indique 486,5 km. Calculez la vitesse
moyenne durant le trajet (en m/s et en km/h).
5. Lors d'une épreuve contre Ia montre de 20 km, un cycliste par-
court les 10 premiers kilomètres à 40 km/h de moyenne. Les 10
derniers sont en côte et il les franchit à 20 km/h de moyenne.
Quelle est sa vitesse moyenne sur I'ensemble de I'épreuve ?
Des exercices pour s'entraîner
6. Convertissez les vitesses suivantes en m./s :
108 km/h, 1000 km/h.
7. Une limace rampe sur une distance de 20 cm en 2 minutes.
Exprimer sa vitesse moyenne en m/s et en km/h.
Cinématique 11

8. Hakkinen occupait en 1999 Ia pole position du grand prix
d'Allemagne. Il avait, au cours des essais, effectué un tour du
circuit d'Hockenheim (long de 6,823 km) en 1 min 42,950 s.
Yérifrez qu'il a roulé, durant ce tour, à Ia vitesse moyenne
d'environ 239 km/h.
Des exercices plus difficiles
9. Calculez une valeur approximative de la vitesse moyenne de
l'écolier de I'exemple 2 (celui qui part de chez lui à 7 h 55 min).
10. Un mobile parcourt un kilomètre à 200 km/h, puis un kilomètre
à 20 km/h. Quelle est sa vitesse moyenne sur l'ensemble du
trajet ?
11. Parti le 9 juin 2003 pour les 42,195 km du marathon d'Édim-
bourg, Lloyd Scott, un ancien pompier de 41 ans, a finalement
franchi la ligne d'arrivée le 15 juin aux environs de midi, après
6 jours 4 heures 30 minutes 56 secondes d'efforts. Les journaux
relatent qu'il a marché environ I h par jour, à la vitesse
moyenne de 800 m/h. À sa décharge, il faut préciser qu'il était
vêtu d'un scaphandre de 60 kg et que sa " performance ', (le
record du monde de lenteur) lui a servi à recueillir des fonds
pour une association s'occupant d'enfants leucémiques (il a lui-
même subi en 1989 une transplantation de moelle osseuse à la
suite d'une leucémie).
Yérifiez que la vitesse moyenne donnée correspond bien à la
réalité et calculez la vitesse moyenne pour I'ensemble de
l'épreuve.
12. Lors de l'Ironman de Malaisie du 23 février 2003, le vainqueur,
Luc Van Lierde, a d'abord nagé les 3,8 km en 47 min 54 s. Il a
ensuite mis 53 s pour se changer une première fois, enfourché
sa bicyclette et roulé pendant 4h 47 min 02 s pour parcourir
les 180,2 km prévus. Finalement, après s'être changé en 1 min
55 s, il a couru les 42,2 derniers kilomètres de l'épreuve en 2h
59 min 33 s. Calculez sa vitesse moyenne pour chacune des
épreuves et pour l'ensemble du triathlon.
12 1. Généralités

ns ggg exercices
Remarque générale :
En général, les
r s,E i ri, " ; ;:
" ;; ;:,: ;i;,:;: i: ::,; : :;", 3 c h i ffr e s s is n i fi c a t i fs
Ainsi, dans la r(
IlgO nr_ior"J ,Joo:r, 2 du prem:r chapitre, IIgg est arrondi à
arrond,i a o,ooilreponse 7 du même "ioptirn, o,oor 666 6... est
Rapperons qu'on arrond,it à r,unité supérieure à, partir d.e 5.
Chapitre 1
1. 20 m/s; 1,89 rnls ; 30 000 m/s.
2. 86 km/h ; 1190 km/h.
3. S,59 m/s = 20,Lkm/h.
4. 19,5 m/s = 70,2kmlh.
b. 26,T km/h = T,4l nt/s.
6. B0 ; 279 (m/s).
7. 0,001 67 rn/s = 0,006 01 km/h.
8. G6,B m/s = 2Bg km/h.
9. d _ 920 h, V_1m/s(8,6gkm/h).
10. 10,1 rnls = 86,4 km/h.
11. S,
:j'i j;,"",3*rli*HJî:3^:}if:ti:.:Â,.i'iiiîi::
L'inrormaff;'l:#lïi:,ffi#l'" ro" ra marche) ae n|";i:
u movenne (de l'épreuve) = 0,078; H::iffnffi"t .o".u.1" l'
" l:f,?-ffi :r,ir:l'*!Yuj,ui,J.* = B8,skm/h ; B,e2m/s=
Chapitre 2
a/ AetB ;bt C ; c/D et E ; d/ B ; e/ D ; f/ D.
X
1.
2.
3. Le 2u: 12 m
pour lequel
graphique.
sont parcourus en 4 s et c,est,le seul graphique
Ia vitesse est positive , "lf" ïst nulle dans le B"
4. v (km/h)
60
40
20
0t (h)
61