Exercice corrigé : Transformateur monophasé - Electromagnétisme

MagnElecPro Electromagnétisme - Corrigé de Chapitre 6 Exercice 7 - 1 -
Corrigé de : Chapitre6. Exercice 7
« Transformateur monophasé usuel en régime alternatif sinusoïdal »
Informations concernant le transformateur:
Section droite du circuit magnétique: S = 30 cm2.
Nombre de spires primaire: N1 = 276.
Conditions nominales:
Tension primaire U1n = 220 V, 50 Hz (1).
Courant secondaire I2n = 16 A.
Résultats d'un essai à vide:
Tension primaire U1v = U1n = 220 V, 50 Hz. Courant primaire I1v = 0,32 A.
Tension secondaire U2v = 33,5 V. Puissance primaire P1v = 29 W.
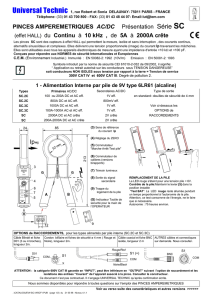
i1
u1 N1
i2
u2
N2
Résultats d'un essai en court-circuit (sous tension primaire réduite):
Tension primaire U1cc = 20 V, 50 Hz. Courant secondaire I2cc = I2n = 16 A.
Puissance primaire P1cc = 43 W.
En régime alternatif sinusoïdal, on peut retenir le modèle suivant :
2
i
1
i
2
u
1
u
fs
L2
r
F
R
1
r
m
1
H
L
m
i1
2
i.m
12 e.me
=
1
e
a) Par définition, le courant secondaire est nul « à vide », donc u)(.)( 12 temt
=
. Le courant primaire à vide est
faible par rapport au courant nominal (en charge « nominale »), donc pour un transformateur industriel usuel :
à vide : )t(e)t(e)t(i.r)t(u 11111 −
≈
−= .
En conclusion : à vide :
1
2
1
1
1
2
)(
)(.
)(
)(
N
N
m
te
tem
tu
tu −=−=
−
=
276
152,0
220
5,33 2
1
2
1
2N
N
N
m
U
U
videà
eff
videà
eff =====⇒
Donc spires 42
2=N
(1) Si rien n'est spécifié, il s'agit des valeurs efficaces.

gnétisme - Corrigé de Chapitre 6 Exercice 7 - 2 -
MagnElecPro Electroma
b) Avec l’hypothèse de Kapp, on modifie légèrement le modèle du transformateur (voir le cours)
2
i.m
1
i
2
u
1
u
m
1
r
1
H
L
F
R
2
r
fs
L2
i
m
i1
12 e.me
=
1
e
On peut ensuite établir un « modèle équivalent ramené au secondaire » (voir le cours) :
Ce modèle est représenté en complexe car le
régime est alternatif sinusoïdal.
2
1m.r
12 E.mE =
2
r
ω
.L.j fs
1
U.m 2
U
2
I
m
I1
s
Z
charge
Si on établit un court-circuit au secondaire :
(
)
2s22fs
2
112 I.ZI.r.L.jm.rU.m0U =++=⇔=
ω
⇒ En court-circuit :
2
1
.
I
Um
Zs=. On en déduit : Ω== 19,0
16
20.152,0
s
Z
c)
()
()
(
)
()
2
1
2
2
2
1
2
fs
2
2
2
1s r.mm.r19,0.Lrm.rZ =>=++=
Ωω
()
Ω
22,8
152,0
19,0
m
19,0
r22
2
1==<⇒
()
Ω==<=⇒
22,8
152,0
19,019,0
22
1
2
1m
rr
Donc lors de l’essai à vide et r. Les pertes Joule sont donc
inférieures à 0,84 W.
W84,032,0.22,8I.r 2
2
v
eff
11 =< 0. 2
22 =
eff
I
La puissance absorbée par le transformateur (Pertes fer + pertes Joule) est de 29 W, donc lors de l’essai à vide
les pertes Joules sont négligeables devant les pertes fer.
Donc lors de cet essai : WPfer 29≈
d) Cette question reprend la démonstration de la « formule de Boucherot » :
Si ).sin()( max tBtB
ω
= :
⇒
()
(
)
(
)
).cos(....
).sin(.
.
).(
.
)(
.
)(
)(.)( max1
max
111
1
111 tBSN
dt
tBSd
N
dt
StBd
N
dt
td
N
dt
td
tirtu
ωω
ω
ϕ
φ
===≈+=

gnétisme - Corrigé de Chapitre 6 Exercice 7 - 3 -
MagnElecPro Electroma
⇒ fBSNBSNU .2...... max1max1
max
1
π
ω
==
⇒ ⇔== 2
.2...
2
max1max
1
1
fBSN
U
Ueff
π
max11 ....44,4 BSfNU eff
=
T
SfN
U
Beff 2,1
10.30.50.276.44,4
220
...44,4 4
1
1
max === −
e) Lors de l’essai en court-circuit: WPWP ccfer 43124,0
220
20.29
2
2
=<<=≈ .
On en déduit que lors de l’essai en court-circuit les pertes fer sont négligeables devant les pertes Joule:
WPJoule 43≈
(
)
ωω
.L.jrZ.L.jrm.r fsssfs2
2
1+==++
Sachant que :
eff
2
eff
1I.mI ≈
(
)
WrIrIrmrIrIrP s
eff
ccs
effeffeff
Joule 4316..... 2
2
2
2
22
2
1
2
22
2
11 ≈==+=+= .
On en déduit : Ω=≈ 168,0
16
43
2
s
r
()
()
(
)
2
fs
2
sfssfs2
2
1s .Lr.L.jr.L.jrm.r19,0Z
ωωω
+=+=++==
Ωω
089,0168,019,0.L 22
fs =−=
f) En fonctionnement nominal :
WPPVU v
fer
eff 29220 11
=
=⇒= ; WPPAI cc
Joule
eff 4316 12
=
=
⇒
=
La chute de tension en charge obtenue par la formule approchée du cours est :
VIXIRUUmU eff
s
eff
s
effeff 69,20.16.089,01.16.168,0)sin(..)cos(... 2222212 =
+
=
+
=−=∆
ϕ
ϕ
Donc VUUmU effeff 75,3069,2220.152,0. 212
=
−
=
∆−= en charge nominale résistive.
Le rendement du transformateur vaut donc :
(
)
()
ferJoule
effeff
effeff
ferJouleondaire
ondaire
PPIU
IU
PPP
P
++
=
++
=
222
222
sec
sec
cos..
cos..
ϕ
ϕ
η
%2,87872,0
29431.16.75,30
1.16.75,30 ==
++
=
η
Rappelons que le rendement des transformateurs de forte puissance apparente (quelques 100 kVA à quelques
100 MVA) est plutôt de l’ordre de 97% à 99%.
1
/
3
100%