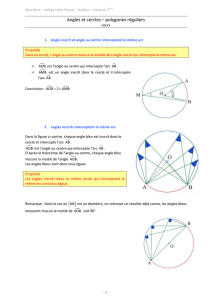
Soit 3 points distincts, A, B, E, situés sur un cercle de centre O

O
A
B
E
1
2
AEB = × AOB
1
2
Fiche de synthèse : ANGLES INSCRITS
ET ANGLES AU CENTRE
Soit 3 points distincts, A, B, E, situés sur un cercle de centre O. À
l’intérieur de ce cercle, on va pouvoir calculer les mesures d’angles
inscrits et d’angles au centre.
Rappel : on appelle angle inscrit, un angle dont le sommet (ici E) se situe
sur un cercle et dont les côtés coupent ce cercle (ici [EA] et [EB]).
On appelle angle au centre, un angle dont le sommet est le centre d’un
cercle (ici O) et dont les côtés coupent ce cercle (ici [OA] et [OB]).
Il est possible de calculer la mesure d’un angle inscrit en connaissant la
mesure de l’angle au centre.
A l’inverse, il est possible de calculer la mesure d’un angle au centre en
connaissant la mesure d’un angle inscrit.
Selon la propriété suivante, si AEB (angle inscrit) et AOB (angle au centre)
interceptent le même arc de cercle (AB), alors AOB = 2 × AEB.
Et donc
Pour pouvoir calculer la mesure d’un angle au centre à partir d’un angle
inscrit (ou vice versa), les deux angles doivent intercepter le même
arc de cercle. Dans le cas présent, AEB et AOB partagent le même arc de
cercle AB.
Il est également nécessaire de connaître la mesure de l’angle inscrit
ou bien de l’angle au centre (selon ce que l’on cherche à calculer).
Ainsi si AOB = 2 × AEB alors AEB = × AOB

E
A
B
O
F
AEB = × 70 = 35°
1
2
A
M
B
O
Par exemple si AOB = 70° alors
Pour ce type de relation, on trouve la conséquence suivante.
Si l’angle au centre AOB devient plat ([AB] est alors le diamètre du
cercle), alors on retrouve le théorème sur les triangles rectangles et
le cercle circonscrit.
Pour tout point M appartenant au cercle et distinct des points A et B, le
triangle AMB sera alors rectangle en M.
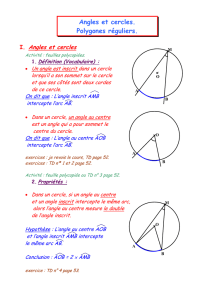
Enfin, prenons un cercle de centre O, sur lequel sont situés les points A, B,
E et F.
Il est possible de calculer la mesure d’un angle inscrit en connaissant la
mesure d’un autre angle inscrit.
En effet selon la propriété suivante, si AEB (angle inscrit) et AFB (angle
inscrit) interceptent le même arc de cercle AB, alors ils ont la même
mesure et AFB = AEB.
Pour pouvoir utiliser cette égalité, il est nécessaire que les deux angles
inscrits interceptent le même arc de cercle. De plus, il est nécessaire
de connaître la mesure d’un autre angle inscrit pour calculer tout autre
angle inscrit.
Par exemple si AFB = 28° alors AEB = 28°

> Les deux angles doivent intercepter
le même arc de cercle
> Il est nécessaire de connaître la mesure de
l’angle inscrit ou de l’angle au centre
> Si AOB = 2 ×AEB alors AEB = ×AOB
1
2
Angles inscrits et angles au centre
> Permet de calculer la mesure d’un angle inscrit en
connaissant celle de l’angle au centre et inversement > Permet de calculer la mesure d’un angle inscrit en connaissant la mesure d’un autre angle inscrit
> Les deux angles doivent intercepter
le même arc de cercle
> Il est nécessaire de connaître la mesure d’un
autre angle inscrit
> Exemple : si AFB = 28° alors AEB = 28°
> Propriété : Si AEB (angle
inscrit) et AFB (angle
inscrit) interceptent le
même arc de cercle AB,
alors AFB = AEB
OA
B
E
E
A
B
O
F
> Propriété : Si AEB (angle
inscrit) et AOB (angle au
centre) interceptent le
même arc de cercle AB,
alors AOB = 2 ×AEB
et AEB = ×AOB
Conséquence
> Si l’angle au centre AOB devient plat
([AB] diamètre du cercle) alors on retrouve
le théorème sur les triangles rectangles
et le cercle circonscrit
> Pour tout point Mappartenant
au cercle et distinct des points A et B,
le triangle AMB est rectangle A
M
B
O
1
2
> Exemple : si AOB = 70° alors AEB = ×70 = 35°
1
2
> Les deux angles doivent intercepter
le même arc de cercle
> Il est nécessaire de connaître la mesure de
l’angle inscrit ou de l’angle au centre
> Si AOB = 2 ×AEB alors AEB = ×AOB
1
2
1
2
Angles inscrits et angles au centre
> Permet de calculer la mesure d’un angle inscrit en
connaissant celle de l’angle au centre et inversement > Permet de calculer la mesure d’un angle inscrit en connaissant la mesure d’un autre angle inscrit
> Les deux angles doivent intercepter
le même arc de cercle
> Il est nécessaire de connaître la mesure d’un
autre angle inscrit
> Exemple : si AFB = 28° alors AEB = 28°
> Propriété : Si AEB (angle
inscrit) et AFB (angle
inscrit) interceptent le
même arc de cercle AB,
alors AFB = AEB
OA
B
E
OA
B
E
E
A
B
O
F
E
A
B
O
F
> Propriété : Si AEB (angle
inscrit) et AOB (angle au
centre) interceptent le
même arc de cercle AB,
alors AOB = 2 ×AEB
et AEB = ×AOB
Conséquence
> Si l’angle au centre AOB devient plat
([AB] diamètre du cercle) alors on retrouve
le théorème sur les triangles rectangles
et le cercle circonscrit
> Pour tout point Mappartenant
au cercle et distinct des points A et B,
le triangle AMB est rectangle A
M
B
O
A
M
B
O
1
2
1
2
> Exemple : si AOB = 70° alors AEB = ×70 = 35°
1
2
1
2