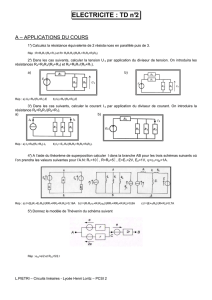
MECANIQUE : TD n°2 - Les CPGE de Loritz

L.PIETRI – Mécanique - Lycée Henri Loritz – PCSI 2
MECANIQUE : TD n°2
A – APPLICATIONS DU COURS
1°) On suppose que le champ de pesanteur g=-ge
z
est uniforme et que les autres forces sont négligés. Un
projectile est lancé à la date t=0 depuis le point O (point origine). Le vecteur vitesse initiale, parallèle au plan (Oxz)
est défini par sa valeur v
0
et l’angle α qu’il fait avec Ox.
a) Déterminer l’équation du mouvement z=f(x).
b) En déduire la portée d’un tel mouvement c’est à dire la distance x
p
lorsque z vaut de nouveau O.
Rép : a) z=-1/2.gx²/v
o
²cos²α+xtanα b) x p =v
o
²sin(2α)/g
2°) En présence de frottements la portée sera t-elle inférieure ou supérieure. Expliquez.
Rép : la portée sera inférieure car la force de frottement s’oppose au mouvement
3°) On suppose le mouvement d’un solide dans un fluide selon l’axe Oz. On supposera la fluide soumis à la
poussée d’Archimède Π
ΠΠ
Π=-Mg, au poids et à la force de frottement fluide modélisé ici par –hv. Démontrer que le
point matériel atteint une vitesse limite dont on donnera son expression.
Rép : v
∞
∞∞
∞
=(m-M)/h.g
4°) On considère un pendule simple de longueur l, retrouvez l’équation différentielle de ce pendule en appliquant le
théorème de la puissance cinétique. En prenant comme conditions initiales θ(0)=θ
0
et dθ/dt(0)=0, donnez la
solution θ(t) de ce mouvement.
Rép : d²θ/dt²+ω
0
²θ=0 où ω
0
²=g/l et θ(t)=θ
0
cos(ω
0
t)
B – TRAVAUX DIRIGES
I - RESISTANCE DE L’AIR – CAS LINEAIRE
Dans le repère terrestre R, un point matériel M de masse m est soumis à la force de pesanteur -mg.e
z
et à
la force de frottement -kv.
1°) Etudier la chute libre (v
0
=0) et mettre en évidence une vitesse limite v
∞
∞∞
∞
et un temps de relaxation τ tel que
v=v
∞
∞∞
∞
(1-e
-t/τ
).
2°) Etudier le tir (v
0
=v
0
cosαe
x
+v
0
sinα e
z
) et établir les équations du mouvement suivantes:
x(t)=v
0
τcosα(1-e
-t/τ
) & z(t)=τ(v
0
sinα+ v
∞
)(1-e
-t/τ
)- v
∞
t
3°) Tracer la trajectoire z(x). Quelle est la principale différence avec le mouvement sans résistance de l’air
Rép : 1°) v
∞
∞∞
∞
=gτ où τ=m/k 2°) On peut noter x(t)=x
max
(1-e
-t/τ
) 3°) z(x)=(V
0
sinα+V
∞
)/V
0
cosα.x+τV
∞
.Ln[1-x/V
0
τcosα]. Ici x possède une
valeur limite qu’il ne peut dépasser quelquesoit t.
II – ENROULEMENT D’UN FIL SUR UN CYLINDRE
Un cylindre de révolution, d’axe vertical, de
rayon R, repose sur un plan horizontal et fixe par
rapport à un référentiel (Ox, Oy, Oz).
On attache une extrémité d’un fil
parfaitement souple, infiniment mince et de masse
négligeable à la base du cylindre, et on l’enroule
plusieurs fois dans le sens trigonométrique autour
de cette base. L’autre extrémité du fil est fixée à
une particule M de masse m, astreinte à glisser sur
le plan horizontal (Oxy). La partie IOM non enroulée
du fil est tendue.
Données numériques : R=0,2m ; m=0,04kg ; l
0
=I
0
M=0,5m ; v
0
=0,1ms
-1
.
1°) A l’instant t=0, on communique à la particule M une vitesse v
0
horizontale à I
0
M et orienté comme
l’indiquent les deux figures ci-après.
On admet que le fil reste tendu au cours du mouvement. A l’instant t, on appelle θ l’angle dont s’est enroulé
le fil et l la longueur IM du fil non encore enroulé.
Le fil étant inextensible, donner la relation entre l, l
0,
R et θ.
2°) Exprimer les composantes de OM suivant les vecteurs unitaires u
r
et u
θ
θθ
θ
en fonction de l
0
, R et θ.
3°) En déduire les composantes de la vitesse v de la particule M suivant les vecteurs u
r
et u
θ
θθ
θ
.
4°) Montrer que la norme v de la vitesse reste constante au cours du mouvement.
5°) Déduire des questions 3°) et 4°) la relation entre θ,
0 0
, , et v .
l R θ
&

L.PIETRI – Mécanique - Lycée Henri Loritz – PCSI 2
6°) Exprimer θ en fonction de t, l
0
, R et v
0
.
7°) Déterminer l’instant final t
f
pour lequel le fil est entièrement enroulé autour d’un cylindre. Effectuer
l’application numérique.
8°) a) Déterminer la tension T du fil en fonction de t, m, l
0
, R et v
0
.
b) En réalité, il y a rupture du fil dès que sa tension dépasse la valeur T
rup
=5.10
-3
N. Déterminer l’instant
t
rup
et l’angle θ
rup
lorsqu’intervient la rupture du fil. Effectuer l’application numérique.
Rép : 1°) l=l
0
-Rθ 2°) OM=Ru
r
+(l
0
-Rθ)u
θ
θθ
θ
3°) v=-
0
( )
r
l R u
θ θ −
uur
& 4°) Appliquez le PFD sur u
r
5°) v
0
=
0
( )
l R
θ θ
−
&
6°) v
0
t=l
0
θ-Rθ²/2⇒ 7°) t
f
=6,25s 8°) a) b) t
rup
=6,09s et θ
rup
=120°
C – EXERCICES SUPPLEMENTAIRES
I – CONDITION DE NON-DECOLLAGE
Une automobile, assimilée à un point matériel, circule à la vitesse v
uniforme, sur une piste au profil accidenté. Elle franchit une bosse,
modélisée par deux portions rectilignes raccordées par un arc de cercle de
rayon l et d’ouverture angulaire 2α.
1°) A quelle condition la voiture garde-t-elle le contact avec le sol
2°) Déterminer la vitesse maximale remplissant cette condition. A.N: α=10°
& l=5m
Rép : 1°) Si v≤√(glcosθ) 2°) v≤√(glcosα)=6,9ms
-1
.
.
II – PLAN INCLINE ET POULIES
Le solide S
1
de masse m
1
=400g, glisse sans frottements sur le plan
incliné. Le solide S
2
de masse m
2
=200g, se déplace verticalement. Les
solides en translation sont considérés comme des points matériels. Les
poulies sont idéales, les fils sont inextensibles et sans masse. (Donnée
α=30°)
1°) On considère le premier dispositif. Déterminez l’accélération du
solide S
2
et la tension du fil.
2°) On rajoute une poulie. La poulie P
2
est fixe, la poulie P
1
se
déplace parallèlement au plan incliné. Le fil est attaché en A. Déterminer
l’accélération du solide S
2
et les tensions du fil.
Rép : 1°) a(S
2
)=(m
1
sinα-m
2
)/(m
1
+m
2
).ge
z
=0 et T
2
=m
1
m
2
/(m
1
+m
2
).(1+sinα)g=1,96N 2°)
a(S
2
)=(2m
1
sinα-m
2
)/(2m
1
+m
2
).ge
z
=1,96ms
-2
e
z
et T
2
=2m
1
m
2
/(2m
1
+m
2
).(1+sinα)g=2,35N
III – MOUVEMENT D’UN POINT MATERIEL SUR UN CERCLE
Un point matériel M de masse m se déplace sans frottements sur un
cercle de rayon a passant par le point O. Il est soumis à la force f=f(r)u
r
avec
OM=ru
r
et à la réaction du support.
1°) Déterminer la fonction f(r) pour que la réaction R exercée par M sur le
cercle soit constante.
2°) Déterminer la relation entre
2
et
θ θ
&
faisant intervenir les conditions
initiales.
3°) Décrire le mouvement du point M dans les différents cas possibles.
Rép : 1°) f(r)=A/r
5
2°) 3°) Tout dépend du signe de la valeur de
la constante A…
2
54
1
32 cos ( )
2
A
K
ma
θθ
= − +
&
0 0
2
0
2
( ) 1 1
l Rv t
tR l θ = − −
1/ 2
2
0 0
2
0 0
2
1
mv Rv t
Tl l = −

L.PIETRI – Mécanique - Lycée Henri Loritz – PCSI 2
C-II) PLAN INCLINE ET POULIES

L.PIETRI – Mécanique - Lycée Henri Loritz – PCSI 2
C-III) MOUVEMENT D’UN POINT MATERIEL SUR UN CERCLE

L.PIETRI – Mécanique - Lycée Henri Loritz – PCSI 2
B-II) ENROULEMENT D’UN FIL SUR UN CYLINDRE