f(x) - Profmath55

Terminale S
Devoir à la maison n°8 : corrigé
________________________________________________________________
_________________________________________________________________________________________________________________
corDM8A10S
Exercice 1 :
On désigne par f la fonction définie sur l’ensemble R des nombres réels par f (x) = 1
1+e
-x
On note C la courbe représentative de f dans un repère orthonormal (unité 5cm)
Partie A. Étude de la fonction f
1. Vérifier que pour tout nombre réel x : f (x) = e
x
1+e
x
f (x) = 1
1+e
-x
= 1
1+e
-x
×
××
× e
x
e
x
= e
x
e
x
+ 1
2. Déterminer les limites de f en −∞ et en +∞. Interpréter graphiquement les résultats obtenus.
En + ∞
∞∞
∞
lim
x→
→→
→+ oo
e
-x
= lim
x→
→→
→- oo
e
x
= 0 d’où lim
x→
→→
→+ oo
(1 + e
-x
) = 1 et par passage à l’inverse, lim
x→
→→
→+ oo
f(x) = 1
La droite d’équation y = 1 est asymptote à la courbe représentative de f en + ∞
∞∞
∞
En - ∞
∞∞
∞
lim
x→
→→
→- oo
e
-x
= lim
x→
→→
→+ oo
e
x
= + ∞
∞∞
∞ d’où lim
x→
→→
→- oo
(1 + e
-x
) = + ∞
∞∞
∞ et par passage à l’inverse, lim
x→
→→
→- oo
f(x) = 0
La droite d’équation y = 0 est asymptote à la courbe représentative de f en - ∞
∞∞
∞
3. Calculer f′(x)pour tout nombre réel x. En déduire les variations de f sur R.
La fonction f est dérivable sur R comme quotient de fonctions dérivables sur R et on a f ’(x) = -(-e
-x
)
(1 + e
-x
)²
soit encore f ’(x) = e
-x
(1 + e
-x
)²
Il est clair que f ’(x) > 0 sur R donc f est strictement croissante sur R.
4. Dresser le tableau des variations de f .
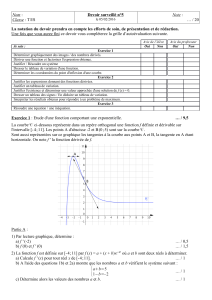
5. Tracer la courbe C et ses asymptotes éventuelles dans le repère
x
f '
f(x)
−∞
−∞−∞
−∞
+
0
+∞
∞∞
∞
1

Terminale S
Devoir à la maison n°8 : corrigé
________________________________________________________________
_________________________________________________________________________________________________________________
corDM8A10S
Partie B. Quelques propriétés graphiques.
1. On considère les points M et M′ de la courbe C d’abscisses respectives x et - x. Déterminer les
coordonnées du milieu A du segment [MM′]. Que représente le point A pour la courbe C ?
les points M et M′ de la courbe C ont pour coordonnées respectives (x ; f(x)) et (-x ; f(-x)).
Alors A
x + (-x)
2
f(x) + f(-x)
2
soit A(0 ;f(x) + f(-x)
2) ie A
0
1
1+e
-x
+ 1
1+e
x
2
A(0 ;0 ,5)
C’est le centre de symétrie.
2. Soit n un entier naturel. On désigne par D
n
le domaine du plan limité par la droite d’équation
y=1, la courbe C et les droites d’équations x = 0 et x = n. A
n
désigne l’aire du domaine D
n
exprimée en unité
d’aire.
a. Calculer A
n.
A
n.
=
⌡
⌠
0
n
(1 - f(x))dx =
⌡
⌠
0
n
[1 - 1
1+e
-x
]dx =
⌡
⌠
0
n
[1+e
-x
1+e
-x
- 1
1+e
-x
]dx= -
⌡
⌠
0
n
-e
-x
1+e
-x
dx = - ln(1+e
-n
) +ln(1+e
-0
)=
ln(2) - ln(1+e
-n
)
b. Étudier la limite éventuelle de A
n
, lorsque n tend vers +∞.
lim
x→
→→
→+ oo
A
n.
= ln2
Partie C. Calcul d’un volume.
Soit λ un réel positif, On note V (λ) l’intégrale
⌡
⌠
-λ
0
π[f(x)]²dx
On admet que V (λ) est une mesure exprimée en unité de volume, du volume engendré par la rotation autour de
l’axe des abscisses, de la portion de la courbe C obtenue pour −λ ≤ x ≤ 0.
1. Déterminer les nombres réels a et b tels que pour tout nombre réel x : e
2x
(e
x
+ 1)² = ae
x
e
x
+ 1 + be
x
(e
x
+ 1)²
e
2x
(e
x
+ 1)² = ae
x
e
x
+ 1 + be
x
(e
x
+ 1)² ⇔
⇔⇔
⇔ e
2x
(e
x
+ 1)² = ae
x
e
x
+ 1 ×
××
× e
x
+ 1
e
x
+ 1 + be
x
(e
x
+ 1)² ⇔
⇔⇔
⇔ e
2x
(e
x
+ 1)² = ae
2x
+ ae
x
(e
x
+ 1)² + be
x
(e
x
+ 1)²
⇔
⇔⇔
⇔ e
2x
(e
x
+ 1)² = ae
2x
+ (a + b)e
x
(e
x
+ 1)² ⇔
⇔⇔
⇔ e
2x
= ae
2x
+ (a + b)e
x
⇔
⇔⇔
⇔
a = 1
a + b = 0 ⇔
⇔⇔
⇔
a = 1
b = - 1
Finalement e
2x
(e
x
+ 1)² = e
x
e
x
+ 1 – e
x
(e
x
+ 1)²
2. Exprimer V (λ) en fonction de λ.
V (λ) =
⌡
⌠
-λ
0
π
ππ
π[f(x)]²dx = π
ππ
π
⌡
⌠
-λ
0
e
x
1+e
x
² dx = π
ππ
π
⌡
⌠
-λ
0
e
x
1+e
x
² dx = π
ππ
π
⌡
⌠
-λ
0
e
2x
(e
x
+ 1)²dx = π
ππ
π
⌡
⌠
-λ
0
[ e
x
e
x
+ 1 – e
x
(e
x
+ 1)²]dx
= π
ππ
π
⌡
⌠
-λ
0
e
x
e
x
+ 1dx – π
ππ
π
⌡
⌠
-λ
0
e
x
(e
x
+ 1)²dx = π
ππ
π [ln(e
x
+ 1)]
-λ
λλ
λ
0
+π
ππ
π [ 1
e
x
+1]
-λ
λλ
λ
0
=π
ππ
π[ln(2) - ln(e
-λ
λλ
λ
+ 1) + 1
2 – 1
e
-λ
λλ
λ
+1]
3. Déterminer la limite de V (λ) lorsque λ tend vers +∞
lim
lambda→
→→
→+ oo
V (λ) = π
ππ
πlim
lambda→
→→
→+ oo
(ln(2) - ln(e
-λ
λλ
λ
+ 1) + 1
2 - 1
e
-λ
λλ
λ
+1) = π
ππ
πln(2) - 1
2π
ππ
π
Exercice 2 :
Partie A. Restitution organisée de connaissances
Prérequis : On rappelle les deux résultats suivants.
R1 : Si z est un nombre complexe non nul, on a l’équivalence suivante :
|z| = r et arg z = θ [2π] ⇔ z = r (cosθ + isinθ) et r > 0
R2 : Pour tous nombres réels a et b :
cos(a + b) = cos a cosb − sin a sinb et sin(a + b) = sin a cosb + sinb cos a
Soient z1 et z2 deux nombres complexes non nuls.
Démontrer les relations : |z
1
× z
2
| = |z
1
||z
2
| et arg(z
1
× z
2
) = arg(z
1
) + arg(z
2
) modulo 2π
z
1
×
××
× z
2
= r
1
(cosθ
1
+ isinθ
1
) ×
××
× r
2
(cosθ
2
+ isinθ
2
) = r
1
×
××
× r
2
×
××
× (cosθ
1
+ isinθ
1
)×
××
× (cosθ
2
+ isinθ
2
)
z
1
×
××
× z
2
= r
1
×
××
× r
2
×
××
× (cosθ
1
cosθ
2
+ i cosθ
1
sinθ
2
) + (isinθ
1
cosθ
2
+ i ²sinθ
1
sinθ
2
)

Terminale S
Devoir à la maison n°8 : corrigé
________________________________________________________________
_________________________________________________________________________________________________________________
corDM8A10S
z
1
×
××
× z
2
= r
1
×
××
× r
2
×
××
× (cosθ
1
cosθ
2
+ i cosθ
1
sinθ
2
+ isinθ
1
cosθ
2
- sinθ
1
sinθ
2
)
z
1
×
××
× z
2
= r
1
×
××
× r
2
×
××
× (cosθ
1
cosθ
2
- sinθ
1
sinθ
2
)+ i( cosθ
1
sinθ
2
+ sinθ
1
cosθ
2
)
z
1
×
××
× z
2
= r
1
×
××
× r
2
×
××
×[ cos(θ
1
+ θ
2
) + isin(θ
1
+ θ
2
)]
alors
|z
1
×
××
× z
2
| = r
1
×
××
× r
2
= |z
1
||z
2
|
arg(z
1
×
××
× z
2
) = (θ
1
+ θ
2
) modulo 2π = arg(z
1
) + arg(z
2
) modulo 2π
Partie B.
Pour chaque proposition, indiquer si elle est vraie ou fausse et proposer une démonstration pour la réponse
indiquée. Dans le cas d’une proposition fausse, la démonstration consistera à fournir un contre-exemple. Une
réponse sans démonstration ne rapporte pas de point.
On rappelle que si z est un nombre complexe, z désigne le conjugué de z et |z| désigne le module de z.
z = - 1
2 + 1 2i = 1 2
( )
-1 + i = 2
2
- 2
2 + 2 2i= 2
2 e
4
π −
i
donc z
4
= 4
16 e
i(-π
ππ
π)
= - 1
4 réel VRAI
z + z = 0 ⇔
⇔⇔
⇔ (a + ib) + (a – ib) = 0 ⇔
⇔⇔
⇔ 2a = 0 ⇔
⇔⇔
⇔ a = 0 et b quelconque FAUX
z + 1
z = 0 ⇔
⇔⇔
⇔ z² + 1
z = 0 ⇔
⇔⇔
⇔ z² + 1 = 0 ⇔
⇔⇔
⇔ z = i ou –i VRAI
si z = e
4
π −
i
alors |z| = 1 et si z’ = 1 alors z + z’ = e
4
π
i
d’où |z + z’| = 1 FAUX