101 Groupes monogenes, groupes cycliques

101
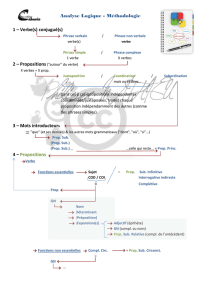
Groupes monogènes, groupes cycliques, exemples.
Tout groupe cyclique d'ordre
n * (resp. monogène) est
isomorphe à /n (resp. ).
Reversat, De Biasi,
Gourdon Alg+An.
Lanzmann.
I. Groupes monogènes (Reversat p.19-20).
A. Définitions et caractérisations.
(
)
,.
G
{
}
tq. /
k
x G G x x k∃ ∈ = = ∈
(
)
,.
G
(
)
, 1
+ =
( )
/ , 1
n+ = 
{
}
* / 1
n
n
U z z
= ∈ =
(
)
,
n
U
×
(
)
*,
×
(
)
*,
×
p
a e
=
{
}
1
; ;...; p a e a a
−
=
(
)
(
)
|
o a o G
B. Générateurs.
(
)
n
ϕ
1
k n
∧ =
1; 1
k n
∈ −
(
)
,
n
U
×
2
ik
n
k
e
π
ω =
1
k n
∧ =
G a
=
a
1
a
−
II. Exemples de groupes monogènes ou
cycliques.
A. Sous-groupes. (Reversat/Lanzmann)
0
3
{
}
3 0; 3
=
2
{
}
2 0; 2; 4
=
(
)
,
n
U
×
2i
d
e
π
B. Produit de deux groupes. (Gourdon p.23)
1
m n
∧ =
C. Exercices. (Gourdon p.39)
III. Notes.

xxx TITRE DE LA LEÇON Développement Bibliographie