énoncé

Spé ψ
ψψ
ψ 2015-2016 page 1/5 Devoir n°7
Spé ψ
ψψ
ψ 2015-2016 Devoir n°7
ONDES-CHIMIE
P ARTIE I
L’espace est rapporté à un triangle rectangle direct Oxyz et l’on désigne par
, et
x y z
e e e
les
vecteurs unitaires des axes.
1) On se place dans le vide, en l’absence de charges et courants.
a) Établir l’équation de propagation du champ électrique
( )
,
E M t
.
b) On suppose que les champs cherchés ne dépendent que de la coordonnée spatiale z
(les dérivés partielles des champs par rapport à x et y sont nulles). Écrire les équations aux dérivées
partielles auxquelles obéissent les composantes du champ électrique.
Pour chaque composante, la solution de cette équation est la somme de deux termes. À quoi
correspondent-ils ?
c) On considère un de ces deux termes. Montrer que l'onde correspondante est trans-
versale et exprimer sa vitesse de propagation, notée c en fonction de ε
0
et µ
0
, respectivement la
permittivité électrique et la perméabilité magnétique du vide.
d) On considère le champ électrique
( )
11
, cos
x
z
E z t E t e
c
= ω − . Déterminer l'ex-
pression du champ magnétique d'amplitude B
1
. Préciser le rapport E
1
/B
1
.
e) On considère le champ électrique
( )
22
, cos
x
z
E z t E t e
c
= ω + . Déterminer
l'expression du champ magnétique d'amplitude B
2
. Préciser le rapport E
2
/B
2
.
2) Une onde électromagnétique progressive plane se propage dans le
vide vers un plan métallique parfaitement conducteur et normal à la direction
de propagation qui se fait selon la direction Oz dans le sens de
z
e
. Le métal
est situé dans la région des z > 0. La géométrie du système est donnée ci-
contre.
On rappelle que la composante tangentielle d’un champ électrique est
continue à la traversée d’une interface.
On considère une onde incidente
( )
I
, cos
x
I
z
E z t E t e
c
= ω − . On admet que le champ
électrique est nul à l'intérieur du métal et que le champ magnétique n'y possède pas de composante
variable dans le temps.
a) Montrer qu'une onde réfléchie prend naissance à la surface du conducteur.
b) Exprimer les vecteurs
R
E
et
R
B
de cette onde réfléchie en fonction de E
I
, ω, t, z,
c,
x
e
et
y
e
.
c) Exprimer les champs résultants
E
et
B
en un point de coordonnée z < 0 où
coexistent onde incidente et onde réfléchie.
d) Quel type d'onde obtient-on?
3) On crée un oscillateur en disposant dans le vide
deux plans parallèles parfaitement conducteurs selon la
géométrie ci-contre.
On se place dans l'approximation des ondes planes.
On admet qu'un système d'ondes stationnaires existe dans le
y
e
⊙
z
z
= 0
z
> 0
CONDUCTEUR
PARFAIT
VIDE
z
e
x
e
z
z
= 0
z
> 0
CONDUCTEUR
PARFAIT
CONDUCTEUR
PARFAIT
z
= –L
VIDE
CAVITE
RESONANTE
y
e
⊙
z
e
x
e

Spé ψ
ψψ
ψ 2015-2016 page 2/5 Devoir n°1
volume délimité par les deux plaques. On raisonne sur un volume cylindrique d'axe z, délimité par
les deux plans et de section unité.
a) Montrer que ce dispositif impose une quantification de la pulsation des ondes pou-
vant s’établir dans la cavité ω
n
= n ω
0
où n est un entier. Expliciter ω
0
en fonction de c et L.
b) En déduire que pour l’onde de pulsation ω
n
= n ω
0
, le champ électrique
(
)
,
n
E z t
dans la cavité prend la forme
(
)
(
)
(
)
, sin sin
n
x
E z t A z t e
= α β en explicitant A, α et β en fonction de
E
I
, ω
0
, c et n.
c) Exprimer la densité volumique d'énergie électrique w
E
et la densité d'énergie ma-
gnétique w
M
du champ électromagnétique en fonction de z. On prendra pour expressions de
E
et
B
celles obtenues à la question 2-c.
d) En intégrant ces grandeurs sur le volume défini ci-dessus, exprimer l'énergie élec-
tromagnétique totale en fonction de L, E
I
et ε
0
. Montrer qu'elle est constante.
e) Montrer qu'il y a échange permanent entre énergie électrique et énergie magnéti-
que.
4) On étudie maintenant une onde telle que, entre les plaques, le champ électrique s’écrit
( )
0
sin cos
y
z
E E t kx e
L
π
= ω −
avec k réel.
a) Cette onde est-elle progressive ? Peut-on définir une direction de propagation ?
L’onde est-elle transverse électrique ? Les conditions aux limites sont-elles vérifiées ? Imposent-
elles une condition de quantification ? L’onde est-elle transverse magnétique ?
b) L’équation de propagation montrée en I-1-a étant toujours vérifiée (le milieu est
toujours le vide entre les plaques), établir la relation de dispersion du phénomène.
c) Montrer qu’il existe une pulsation de coupure ω
C
et préciser cette notion.
d) Exprimer vitesse de phase et vitesse de groupe de l’onde en fonction de c, ω et ω
C
.
Commenter ces résultats.
P ARTIE II
De par ses propriétés physiques et chimiques, l’élément aluminium est un composé très pré-
sent dans notre environnement moderne. Il est en particulier utilisé dans la fabrication des guides
d’onde et cavité résonantes étudiées dans la première partie.
1) Utilisation de l’aluminium pour les structures métalliques :
Pourquoi l’aluminium est-il couramment utilisé pour les cadres de vélo, les structures de
remorque, les lignes électriques à haute tension, etc ?
2) Étude cristallographique de l’aluminium :
L’aluminium comme de nombreux métaux cristallise suivant la structure cubique à face
centrée.
a) Représenter l’allure d’une maille élémentaire.
b) Comment s’effectue le contact entre les atomes ? En déduire la relation entre le
paramètre de maille a et le rayon atomique R
Al
.
c) Combien y a-t-il d’atomes par maille ?
d) Définir la compacité C puis l’évaluer numériquement.
e) Soient M la masse molaire de l’aluminium, R
Al
son rayon atomique, N
A
le nombre
d’Avogadro et ρ
Al
la masse volumique de l’aluminium, déterminer la relation entre M, R
Al
, N
A
et
ρ
Al
. Application numérique : évaluer la densité d
Al
de l’aluminium.
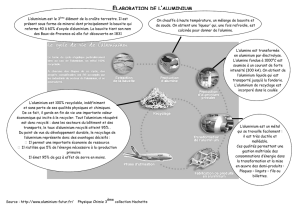
3) Préparation de l’aluminium
La bauxite contient environ 55% en masse d'alumine Al
2
O
3
.En simplifiant une réalité com-
plexe, on considère que l'électrolyse de l'alumine fondue (à 950°C) met en jeu les processus redox
suivants (électrodes en carbone) :

Spé ψ
ψψ
ψ 2015-2016 page 3/5 Devoir n°1
O
2–
→ 1/2 O
2(G)
+ 2 e
–
Al
3+
+ 3 e
–
→ Al
(S)
a) Sachant que l’aluminium se trouve dans la 13
e
colonne, et 3
e
période de la classifi-
cation périodique des éléments, décrire la configuration électronique de l’aluminium. Quel est son
degré d’oxydation maximal ? Justifier que l’alumine Al
2
O
3
est une forme oxydée de l’aluminium.
b) Indiquer quels processus se produisent à l’anode et à la cathode.
c) Écrire l'équation bilan de l'électrolyse.
d) Quelle est la masse de bauxite à extraire pour produire 1 tonne d'aluminium?
e) Quelle est l'énergie consommée par tonne d'aluminium produite si U = 4,5 V ?
4) Détermination expérimentale de constantes d’équilibre :
On considère les équilibres chimiques suivants de constantes d’équilibre K
S
et β :
Al(OH)
3(S)
= Al
3+
+ 3 OH
–
K
S
Al
3+
+ 4 OH
–
= Al(OH)
4–
β
a) Comment nomme-t-on ces deux constantes d’équilibre K
S
et β ? Comment
nomme-t-on le complexe Al(OH)
4–
?
b) On considère l’équilibre thermodynamique suivant :
Al(OH)
3(S)
+ OH
–
= Al(OH)
4–
, de constante d’équilibre K. Exprimer K en fonction de K
S
et
de β .
On réalise le dosage, suivi par pHmétrie, de 40 mL d’une solution aqueuse d’acide nitrique à
0,1 mol⋅L
–1
et de sulfate d’aluminium (2 Al
3+
, 3 SO
42–
) de concentration c inconnue, par de la soude
à 1 mol⋅L
–1
.
c) Faire un schéma du dispositif du dosage et nommer la verrerie utilisée.
d) Quelle grandeur physique, mesurée par le pHmètre, est l’image du pH de la solu-
tion ?
La figure 1 donne le pH de la solution titrée en fonction du volume de soude versé. On peut
distinguer différentes étapes au cours de ce titrage.
Pour V = 3,7 mL, on a pH = 3,7 et pour V = 13,8 mL, on a pH = 11,2.
Observations :
Etape 1 : 0 < V < 3,7 mL, la solution est claire et limpide.

Spé ψ
ψψ
ψ 2015-2016 page 4/5 Devoir n°1
Etape 2 : 3,7 mL < V < 13,8 mL, la solution devient de plus en plus trouble.
Etape 3 : 13,8 mL < V < 17,2 mL, à la fin de cette étape, la solution est à nouveau claire et
limpide.
e) Associer à chacune de ces étapes une réaction prépondérante.
f) Évaluer la concentration c en sulfate d’aluminium de la solution utilisée.
g) En déduire les valeurs des deux constantes d’équilibre Ks et β . On donnera aussi
les valeurs de pK
S
et de log
10
( β ).
Dans la suite du problème, on admettra que pKs = 32 et que log
10
( β ) = 34.
5) Diagramme E-pH de l’aluminium :
Les espèces chimiques envisagées ici sont Al(OH)
3(s)
, Al
3+
, Al
(s)
et Al(OH)
4–
.
On donne le diagramme potentiel-pH de l’aluminium à 298 K, pour une concentration totale
en espèces dissoutes de 10
–2
mol.L
–1
(figure 2).
Le point A a pour ordonnée : E = – 1,71 V, le point B a pour abscisse pH
B
= 10.
a) Préciser le degré d’oxydation de l’aluminium dans chacune des espèces envisagées
et attribuer à chacun des quatre domaines numérotés de 1 à 4 l’espèce qui lui est rattachée.
b) Préciser les valeurs des pentes du segment séparant les espèces 3 et 4.
c) Déterminer la valeur du potentiel standard E°(Al
3+
/Al).
d) Définir en quelques mots les termes : passivation, immunité et corrosion. Attribuer
à chacun de ces termes une zone dans le diagramme E-pH.
e) Par ajout de poudre d’aluminium dans une solution d’acide concentrée, on assiste
à une vive réaction accompagnée d’un dégagement gazeux . De quel gaz s’agit-il ? Préciser
l’équation bilan de cette réaction. Justifier cette observation par le tracé qualitatif de courbes
I = f(V) convenablement choisies
f) Peut-on laisser sans protection particulière une barre d’aluminium en contact avec
de l’eau de pluie ?
6) Aluminothermie :
Le soudage par aluminothermie consiste à générer un très fort dégagement d’énergie ther-
mique par réaction de poudre d’aluminium sur un oxyde métallique. Le métal en fusion permet
alors de réaliser des soudures de grande qualité. Cette technique est particulièrement bien adaptée
au soudage des rails de chemin de fer.

Spé ψ
ψψ
ψ 2015-2016 page 5/5 Devoir n°1
On considère la réaction chimique : Fe
2
O
3(S)
+ 2 Al
(S)
= 2 Fe
(S)
+ Al
2
O
3(S)
.
a) Déterminer l’enthalpie standard de réaction, ∆
r
H°(298 K), de la réaction précé-
dente. Commenter son signe.
b)Lorsqu’on mélange dans un creuset de l’oxyde de fer (III) et de la poudre
d’aluminium dans des proportions stœchiométriques, après un amorçage de la réaction, celle-ci est
extrêmement violente et peut être considérée comme totale et instantanée. Pour justifier qu’il y a
effectivement fusion des phases solides, on se propose d’évaluer un ordre de grandeur de la tempé-
rature atteinte par le mélange en fusion en fin de réaction. On adopte un modèle simple dans lequel
on néglige la capacité thermique du creuset et on considère le système comme adiabatique. Déter-
miner dans ces conditions la température T des produits obtenus. Justifier qu’il y a effectivement eu
fusion des produits de la réaction.
c) Dans le cadre du soudage des rails de chemin de fer, quel(s) phénomène(s) physi-
que(s) est (sont) à l’origine de la solidification du cordon de soudure ?
Formulaire de physique
(
)
(
)
(
)
(
)
(
)
rot rot grad div
A A A
= − ∆
Dans la base cartésienne :
( )
rot
y y
x x
z z
x y z
A A
A A
A A
A e e e
y z z x x y
∂ ∂
∂ ∂
∂ ∂
= − + − + −
∂ ∂ ∂ ∂ ∂ ∂
( ) ( )
cos cos 2cos cos
2 2
a b a b
a b
+ −
+ =
( ) ( )
cos cos 2sin sin
2 2
a b a b
a b
+ −
− = −
(
)
(
)
(
)
2 2
cos sin 2cos 2
x x x
− =
Données pour la partie chimie :
Masse molaire : Al : 27 g⋅mol
–1
; O = 16 g⋅mol
–1
; H = 1 g⋅mol
–1
.
Rayon atomique de l’aluminium : R
Al
= 143 pm.
Nombre d’Avogadro : N
A
= 6,02×10
23
mol
–1
.
On rappelle que l’acide nitrique est un mono acide fort, c’est-à-dire qu’il se dissocie entièrement
dans l’eau.
On a : E°(H
+
/H
2
) = 0 V ; E°(O
2
/H
2
O) = 1,23 V.
On admettra que : RT/ F ln(x) = 0,06log(x) avec R la constante des gaz parfaits, T la température et
F la constante de Faraday.
On donne à 298 K : ∆
f
H°(Al
2
O
3
) = –1 673 kJ⋅mol
–1
; ∆
f
H°(Fe
2
O3) = –824 kJ⋅mol
–1
.
À toute température, on a : Cp°(Fe(s)) = Cp°(Fe
(l)
) = 25 J⋅K
–1
⋅mol
–1
;
Cp°(Al
2
O
3(S)
) = Cp°(Al
2
O3
(l)
) = 120 J⋅K
–1
⋅mol
–1
.
∆ H
FUS
(Al
2
O
3
) = 110 kJ⋅mol
–1
et T
FUSION
= 2050°C ; ∆ H
FUS
(Fe) = 15 kJ⋅mol
–1
et T
FUSION
= 1535°C.