Document

Cours 07 – Cinématique du point SSI 2ème année
1
Équations horaires
Objectif :
Déterminer les équations horaires d’un solide en translation, en rotation.
-1,5
-1
-0,5
0
0,5
1
1,5
2
2,5
3
3,5
0 0,5 1 1,5 2 2,5 3 3,5 4
Temps ( s )
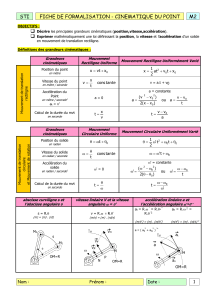
EQUATIONS: POSITION,VITESSE,ACCELERATION DU POINT G
p1(bâti-1 / plateau-1) ( m )
v1(bâti-1 / plateau-1) ( m/s )
a1(bâti-1 / plateau-1) ( m/s² )
X
Y
Fig. 1
Fig. 2
Fig. 3
+ G
+ G
+ G
PHASE 1
PHASE 2
PHASE 3

Cours 07 – Cinématique du point SSI 2ème année
2
Sommaire
1 – Objectif ......................................................... 3
2 – Équations d’un mouvement de translation rect. Unif. .… 3 - 6
3 –Equations d’un mouvement de translation MRUV .......... 6 - 9
4 –Mouvement de rotation …. .................... . . . . . . . . . . . . . . . . . . 9
4.1 – MCU ....................................................... 9 - 10
4.2 – MCUV ….................................................. 10
4.3 – Relation entre V et ................................. 11
5- Accélération normale et tangentielle ........................ 11 - 12
5.1 – Représentation .............................................. 12

Cours 07 – Cinématique du point SSI 2ème année
3
1-Objectif :
Lorsqu’on aborde la partie concernant le déplacement d’un organe (l’actionneur étant soit un vérin
soit un moteur), celui-ci muni d’une charge, en translation rectiligne ou en rotation autour d’un axe
va faire intervenir pour son dimensionnement de nombreux critères ; en particulier, citons les
caractéristiques mécaniques telles que couple ou effort, mais aussi la loi de conduite temporelle.
C’est ce dernier point qui nous intéresse aujourd’hui !!
Les lois de conduites temporelles permettent au travers de leurs graphes de visualiser le
comportement en vitesse de l’actionneur, elles sont nombreuses et variés chacune disposant
d’avantages et d’inconvénients, citons en quelques unes :
*Source : revue TECHNOLOGIE 111 _ JANVIER-FÉVRIER 2001
2- Équations d’un mouvement de translation
rectiligne uniforme.
Le plus simple car il se caractérise par une vitesse de déplacement uniforme. Soit le repère ( o,x,
y ), le point G décrit au cours du mouvement de translation rectiligne une droite d’axe x.
Rail
gradué
Sens du mouvement
Bille
Bloc
moteur
0 m
1 m
Zone
d’accélération
Zone où la vitesse
est constante
O
Le chronomètre est déclenché lorsque
la bille passe au niveau du point O.

Cours 07 – Cinématique du point SSI 2ème année
4
L’image ci-dessous nous montre qu’à chaque intervalle de temps le déplacement est
‘’quasiment’’ le même (sauf marge d’erreur pouvant s’expliquer par la qualité du pointage vidéo).
La position
La Vitesse
Il est donc possible de
traduire cette trajectoire
par une courbe nous
permettant de connaître
la position de la boule en
fonction du temps.
L’équation de cette
courbe est donc une
droite de la forme :
X(t)= d(t) = a.t +b
ou
a = V (vitesse, d=V.t)
b = cte
correspondant à la
position du solide / à la
ligne de départ au
moment du départ ici b
sera égal à « 0 ».
X(t)= d(t) = V0.t
L’allure de la courbe le
confirme, la vitesse reste
la même, la fonction
mathématique sera donc
de la forme :
V(t)= Cte = V0
ou V0 (vitesse, V=d/t)
En allant plus loin on
s’aperçoit que l’équation
horaire de la vitesse
correspond à la dérivée
de la fonction X(t) :
X’(t)= V(t) = V0

Cours 07 – Cinématique du point SSI 2ème année
5
L’accélération
- Résumé.
Pour définir un mouvement il est nécessaire de définir au préalable deux repères :
- Un repère d’espace
- Un repère de temps
Ce mouvement est appelé Mouvement Rectiligne Uniforme ou M.R.U , il se caractérise par le
fait que la vitesse du solide reste constante . Les équations permettant de donner la position, la
vitesse et l’accélération répondent aux solutions suivantes :
- Conditions initiales au moment du départ :
Equation horaire de la position :
X (t) = Vo.t + Xo Xo : position du point à l’instant t = 0 (moment du
départ)
Equation horaire de la vitesse :
X ‘(t) = Vo Vo = constante vitesse à l’instant t = 0 (moment du départ)
Accélération du mouvement : X ‘’(t) = 0
M.R.U
Nota : chaque terme pouvant être positif,
négatif ou nul suivant le repère.
L’allure de la courbe le
confirme, l’accélération
reste quasiment nulle, la
fonction mathématique
sera donc de la forme :
a(t)= 0
En allant plus loin on
s’aperçoit que l’équation
horaire de l’accélération
correspond à la dérivée
seconde de la fonction
X(t) ou à la dérivée de la
vitesse :
a(t)=X’’(t)= dX’(t)/dt
soit
a(t)= 0
Sur la ligne
Après la ligne
Avant la ligne
Départ
Valeur de x0 pour les 3 cas
suivant :
-X0
+ X0
X0 = 0