plan detaille chap3

Chapitre 3 : Le marché en équilibre partiel
I, Les acteurs : les producteurs et les consommateurs
A, La production
1, La fonction de production
a, définition
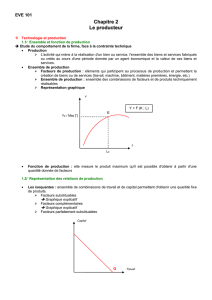
•Le concept de fonction de production
Y = F (X1, X2...Xn)
•Les rendements d'échelle
Y = F (K, L)
–rendements d'échelle constants : F (λK, λL) = λY
–rendements d'échelle croissants : F (λK, λL) > λY
–rendements d'échelle décroissants : F (λK, λL) < λY
b, Etude d'une fonction de production
Y = F (L)
•Productivités moyenne et marginale
–la productivité moyenne du travail : PM (L) = Y / L
–la productivité marginale du travail : Pm (L) = ΔY / ΔL
•Différents cas de fonction de production à un seul facteur

Cas n°1 : fonction à rendements d'échelle constants
Cas n°2 : fonction à rendements d'échelle croissants
Cas n°3 : fonction à rendements d'échelle décroissants
Cas n°4 : fonction à rendements d'échelle croissants puis décroissants

c, les rendements d'échelle et la productivité marginale
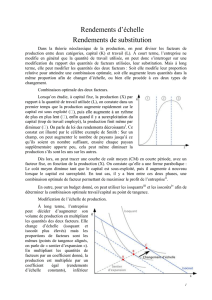
2, L'origine des rendements d'échelle
a, les rendements croissants
•les coûts fixes
•la division du travail
b, Les rendements décroissants ont également plusieurs origines
•les inefficiences liées à la taille de l'entreprise
•la non-homogénéité des facteurs de production
•la disponibilité limitée de certains facteurs de production
3, La fonction de coût
C (Y) = wL
a, le coût marginal et le coût moyen
•le coût marginal : Cm (Y) = Δ C (Y) / Δ Y
•le coût moyen : CM (Y) = C (Y) / Y

b, la relation entre le coût de production et la productivité du travail
4, La fonction d'Offre
a, la fonction d'offre et la maximisation du profit
MAX [ RT – CT ]
b, la concurrence parfaite
MAX [ pY – C (Y) ]
Y
•Recette marginale et prix
Δ R = p Δ Y
Δ R / Δ Y = p
Rm = p
•Prix et coût marginal
Pour rechercher à maximiser le profit, il faut trouver le maximum de la fonction
Π (Y) = [ pY – C (Y) ]
On dérive Π (Y) = pY – C(Y) : Π ' (Y) = p – Cm (Y). Le maximum d'une fonction est établi lorsque
sa dérivée est nulle, Π (Y) admet donc un maximum en p = Cm (Y).
Que se passerait-il si ce n'était pas le cas, par exemple si, pour le niveau de production décidé par

l'entreprise, le prix de marché était supérieur à son coût marginal ? Alors,
p – Cm (Y) > 0
p – Δ C / Δ Y > 0
p Δ Y – Δ C / Δ Y · Δ Y > 0
p Δ Y – Δ C > 0
Cela signifierait que l'entreprise pourrait augmenter son profit en produisant une plus grande
quantité (le profit n'est donc pas, à ce niveau de production, maximisé) : le profit est bien maximum
lorsqu'elle produit une quantité pour laquelle son coût marginal est égal au prix de marché.
•La fonction d'offre et la courbe de coût marginal
CM (Y) = C (Y) / Y donc C (Y) = CM (Y) · Y
Nous avons trouvé un maximum à la fonction Π, il faut vérifier que le profit est alors positif.
Profit positif si : pY – CM (Y) · Y > 0 et donc p > CM (Y) (on simplifie par Y qui est ici strictement
positif). Le profit d'une entreprise est donc maximum lorsqu'elle produit une quantité pour laquelle
le prix de marché est à la fois égal à son coût marginal et supérieur à son coût moyen.