TANGENTE – NOMBRE DÉRIVÉ On note c la représentation

TANGENTE – NOMBRE DÉRIVÉ
On note c la représentation graphique d’une fonction f . A est un point de c (donc y A = ……f (x A) )
I. NOMBRE DÉRIVÉ
Définition 1 La tangente à la courbe c en A est la droite qui passe par A et qui approche le mieux
la courbe c au voisinage de A.
On dit aussi tangente à c au point d’abscisse x A.
Définition 2 Si la courbe c admet au point A une tangente non verticale alors le coefficient directeur de
la tangente est appelé le nombre dérivé de f en x A.
On le note f ′(x A) . On lit : « f prime de x, a ».
On dit que f est dérivable en x A.
Propriété 1 L’équation réduite de la tangente à la courbe c en A est : y = f ′(x A)  (x – x A ) + f (x A).
Exercice 1
La courbe c représente une fonction f.
La droite (TA) est la tangente à la
courbe c en A (– 0,5 ; 8)
Elle recoupe la courbe c en C (4 ; – 2).
La tangente (TB) à la courbe c
en B (2,7 ;– 12,4) est représentée par une
double flèche horizontale.
 La tangente à la courbe c en A ( ou la tangente à la courbe c au point d’abscisse – 0,5 )
n’est pas verticale donc la fonction f est dérivable en ……– 0,5.
Le coefficient directeur de la tangente (TA) est 
 =   =   =    – 2,2
Donc le nombre dérivé de f en ……
– 0,5
est ……
On note f ′ (– 0,5 ) = 
L’équation de (TA) est ……
y = 
 ( x – (– 0,5) ) + 8 soit y =   x – 0,5 + 8 ; y =   x + 7,5
 La tangente (TB) est horizontale donc la fonction f est dérivable en ……2,7
Son coefficient directeur est ……0 donc le nombre dérivé de f en ……2,7 est ……0 On note f ′ ( 2,7 ) = 0
L’équation de (TB) est y = – 12,4
Propriété 2 Le nombre dérivé de f en x A est nul ( f ′(x A) = 0 ) si, et seulement si,
la tangente à la courbe c en A est horizontale
L’équation de cette tangente horizontale est : y = y A ( ou y = f (x A) ).
1/3
(TA)
(T B)
0 1
4
x
y
A
B
C

Exercice 2 Soit f la fonction définie sur [ – 2 ; 2 ] par f (x) = 3 x – x 3 .
On note c sa représentation graphique dans un repère orthonormé (unité graphique : 2 cm ou
bien 2 côtés de grands carreaux)
1) Compléter, à l’aide du tableur de la calculatrice, le tableau ci-dessous puis construire c.
x
– 2
– 1,5
– 1
– 0,5
0
0,5
1
1,5
2
f (x)
2
– 1,125
– 2
– 1,375
0
1,375
2
1,125
– 2
2) On donne f ′(– 0,5) = 9
4 .
a) Compléter : le nombre dérivé de f en ….. – 0,5 est égal à …… 9/4 On note ……f ′ (– 0,5) = 9/4
b) Tracer la tangente (TA) à c au point A d’abscisse – 0,5 puis déterminer l’équation réduite de (TA).
3) La tangente (TB) à c au point B d’abscisse 1 a pour équation y = 2.
T racer (TB) et compléter : le nombre dérivé de f en 1 est égal à 0 On note f ′ (1) = 0
4) La tangente (TC) à c au point C d’abscisse 1,5 a pour équation y = – 3,75 x + 6,75.
Tracer (TC) et compléter : le nombre dérivé de f en 1,5 est égal à ……– 3,75 On note f ′ (1,5) = – 3.75
5) La tangente (TD) à c au point D d’abscisse – 1,5 passe par le point E ( – 1 ; – 3).
Calculer le nombre dérivé de f en – 1,5 puis déterminer l’équation réduite de (TD).
Le nombre dérivé de f en – 1,5 est le coefficient directeur de la droite (DE).
f ′ (– 1,5) = 
 =   =   = - 3,75
L’équation de (TD) est y = – 3,75 (x – (– 1,5) ) – 1,125 soit y = – 3,75x – 5,625 – 1,125 ; y = – 3,75x – 6,75
II. NOMBRE DÉRIVÉ DE FONCTIONS USUELLES
Définition 3 Une fonction trinôme f définie sur  par f (x) = a x 2 + b x + c , avec a  0 .
Sa représentation graphique est une parabole de sommet S d’abscisse x S = – b
2 a .
Si a > 0, la parabole est « tournée vers le haut »
L’ordonnée de S
est y S = f (x S).
Si a < 0, la parabole est « tournée vers le bas »
Si la fonction f admet, pour tout réel x de l’intervalle I, un nombre dérivé, on dit que f est dérivable sur I.
Tableau des dérivées usuelles
fonction f
constante
affine
carré
cube
inverse
trinôme
f (x) =
p
m x + p
x ²
x 3
1/x
a x 2 + b x + c (a  0)
f ′(x) =
0
m
2 x
3 x 2
– 1
x ²
2 a x + b
Exercice 3
f (x) =
x
5 – x
4 x
3
3 x 2 – x + 7
1
7 – x 2
(x – 3) (x + 3) – x 2
f ′(x) =
1
– 1
4/3
6 x – 1
– 2 x
0
2/3
S
S

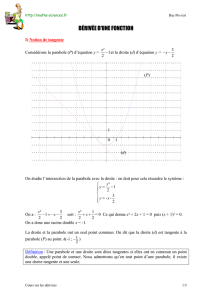
Exercice 4 Soit f la fonction définie sur  par f (x) = 0,5 x 2 – 2 x – 1 .
On note c sa représentation graphique dans un repère orthonormé (unité graphique : le côté d’un grand
carreau pour 1 unité).
1) Déterminer les coordonnées du sommet S de la parabole. Tracer la tangente horizontale.
2) Compléter le tableau puis construire c.
x
– 2
– 1
0
1
2
3
4
5
6
f (x)
5
1,5
– 1
– 2,5
– 3
– 2,5
– 1
1,5
5
3) Calculer f ’(x) .
4) Déterminer une équation de la tangente à cf aux points A et B d’abscisses respectives 2 et 1,5.
Tracer ces tangentes.
5) Construire la droite d d’équation y = 2 x – 1 et déterminer les coordonnées des points où c admet une
tangente parallèle à d .
3/3