vibrations couplees avec le vent - LadHyX

VIBRATIONS COUPLEES
AVEC LE VENT
Pascal Hémon
Laboratoire d’Hydrodynamique, LadHyX
Ecole Polytechnique, Palaiseau
Octobre 2004

Vibrations couplées avec le vent
2
Si vous pensez que j’ai révélé des secrets, je m’en excuse.
Si vous pensez que tout cela n’est qu’un tissu d’absurdité,
Prenez-y plaisir…
Drugpa Künleg (1455-1570)
Pascal Hémon
LadHyX, Département de Mécanique
Ecole Polytechnique
F-91128 PALAISEAU CEDEX
Mél : pascal.he[email protected]lytechnique.fr

3
Avant-propos
L’objectif de ce cours est d’introduire les phénomènes mécaniques produisant les vibrations de
structures sous l’action du vent. Le point de vue adopté est phénoménologique et restreint l’exposé à
des structures bidimensionnelles telles que le profil d’aile, le tablier de pont ou un hauban. Il s’adresse
à un public d’ingénieurs ou d’élèves ingénieur possédant une culture de base en mécanique et
souhaitant appréhender ces problèmes du point de vue physique.
Le premier chapitre expose quelques notions d’aérodynamique de base et pose les définitions qui sont
utilisées ensuite. Ce chapitre constitue principalement une description qualitative des écoulements et
de leurs effets.
Le chapitre 2 est le cœur de ce cours. Il introduit les différents mécanismes générateurs de vibration,
notamment par la notion de dérivées de flottement. L’hypothèse quasi-statique employée permet
d’étudier les différents types d’excitation sans mettre en œuvre des calculs complexes.
Dans le chapitre 3 on s’affranchit de l’hypothèse quasi-statique pour généraliser le domaine
d’application. Les résultats classiques de la théorie de l’aéroélasticité sont présentés et discutés sur le
profil d’aile, puis sur une structure de type tablier.
Enfin le chapitre 4 présente succinctement quelques phénomènes spécifiques rencontrés
essentiellement sur les câbles de hauban.
Ce document s’est enrichi des remarques d’Emmanuel de Langre, Cécile Lemaitre et Charlotte Py du
LadHyX que je remercie pour le temps qu’ils y ont consacré.

5
Sommaire
1. Notions d’aérodynamique ..................................................................7
1.1. Rappels de mécanique des fluides......................................................................7
1.1.1. Equations de Navier-Stokes ................................................................................................. 7
1.1.2. Equations d’Euler.................................................................................................................8
1.1.3. Equation de Bernoulli........................................................................................................... 8
1.1.4. Paramètres adimensionnels ..................................................................................................9
1.1.5. Classification des écoulements........................................................................................... 11
1.2. Les charges aérodynamiques...........................................................................12
1.2.1. Définition des actions de pression et coefficient de pression ............................................. 12
1.2.2. Définition des efforts et des moments aérodynamiques.....................................................13
1.2.3. Le centre de poussée........................................................................................................... 15
1.2.4. Le foyer aérodynamique.....................................................................................................15
1.2.5. Influence du nombre de Reynolds et de la turbulence........................................................ 16
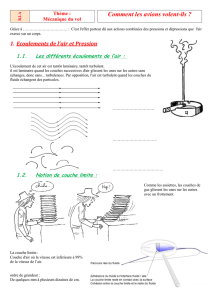
1.3. Le détachement tourbillonnaire.......................................................................18
1.3.1. Description générale........................................................................................................... 18
1.3.2. Le nombre de Strouhal ....................................................................................................... 18
1.3.3. Influence de l’écoulement amont .......................................................................................19
1.4. Le vent turbulent...............................................................................................20
1.4.1. Spectres de turbulence........................................................................................................ 21
1.4.2. Fonctions de cohérence et de corrélation............................................................................22
2. Phénomènes aéroélastiques..............................................................23
2.1. Introduction......................................................................................................23
2.2. La fréquence réduite.........................................................................................24
2.3. Le flottement classique.....................................................................................25
2.3.1. Mise en équation ................................................................................................................25
2.3.2. Stabilité et vitesse critique..................................................................................................27
2.3.3. Cas de l’aile d’avion........................................................................................................... 28