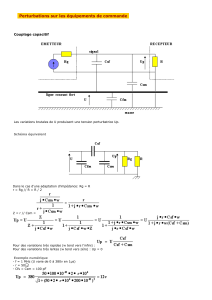
Théorie des modes couplés

Propagation dans un guide d’ondes perturbé –
Théorie des modes couplés
Christophe Sauvan
Table des matières
1 Introduction 3
2 Equation de propagation 4
3 Expression de la solution du problème perturbé en fonction des
modes du guide non-perturbé 5
4 Equation d’évolution des amplitudes Ak(z)6
5 Couplage résonant, codirectionnel et contra-
directionnel 8
5.1 Condition de couplage résonant . . . . . . . . . . . . . . . . . . . . . 8
5.2 Couplage codirectionnel et contra-directionnel . . . . . . . . . . . . . 9
6 Perturbation uniforme en z9
6.1 Equations d’évolution . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
6.2 Résolution des équations d’évolution . . . . . . . . . . . . . . . . . . 11
6.3 Echange d’énergie d’un mode à l’autre . . . . . . . . . . . . . . . . . 12
6.4 Cas particulier du couplage résonant . . . . . . . . . . . . . . . . . . 12
7 Perturbation périodique en z14
8 Annexe A : Expression du champ magnétique 15
9 Annexe B : Orthogonalité des modes 16
1

2

1 Introduction
Le fonctionnement de nombreux composants de l’optique guidée est basé sur
l’utilisation d’une modification ∆nde l’indice de réfraction d’un guide d’onde. Cette
modification peut être locale, uniforme ou périodique suivant l’application visée
(coupleurs directionnels, réflecteurs de Bragg, modulateurs électro-optiques...). La
Figure 1 illustre les principaux types de modification d’indice et les composants qui
les utilisent. Dans la plupart des composants usuels, la modifications d’indice est
faible et peut être traitée comme une perturbation. Dans ce Chapitre, nous dévelop-
pons la théorie des modes couplés qui permet de décrire la propagation de la lumière
dans un guide d’onde perturbé en fonction des modes du guide non-perturbé.
Typede
perturbation
Composants
associés
Filtre réjecteur
(miroirdeBragg)
DiodelaserDBR1
ouDFB2
1Distributed Bragg Reflector 2DistributedFeedBack
Modulateur
électro-optique
Coupleurdirectionnel
Démultiplexeur
De uniformeDe uniformeDe périodique
Typede
perturbation
Composants
associés
Filtre réjecteur
(miroirdeBragg)
DiodelaserDBR1
ouDFB2
1Distributed Bragg Reflector 2DistributedFeedBack
Modulateur
électro-optique
Coupleurdirectionnel
Démultiplexeur
De uniformeDe uniformeDe périodique
Figure 1 – Principaux types de perturbation et composants
associés. La première colonne montre une perturbation périodique
en z. La deuxième colonne montre une perturbation uniforme en
zdue à une modification de l’indice du guide. La troisième co-
lonne montre une perturbation uniforme en zdue à la présence
d’un deuxième guide d’onde.
Tous les exemples de la Figure 1 correspondent au même problème générique,
à savoir la propagation de la lumière dans un milieu inhomogène caractérisé par
une permittivité diélectrique ǫ(x, y, z) qui peut être décomposée comme la somme
d’une permittivité ¯ǫ(x, y) invariante suivant z(le guide d’onde) et d’une perturbation
∆ǫ(x, y, z)≪¯ǫ,
ǫ(x, y, z) = ¯ǫ(x, y) + ∆ǫ(x, y, z).(1)
Cette décomposition est intéressante si les modes du guide non-perturbé caractérisé
par ¯ǫ(x, y) sont connus. Il est important de noter que le système perturbé n’est pas
nécessairement un guide d’onde invariant en z. C’est par exemple le cas avec un ∆ǫ
périodique qui crée un miroir de Bragg, cf. Figure 1. La modification de permittivité
∆ǫpeut être réelle ou complexe, ce qui permet de traiter la présence d’une faible
absorption (Im(∆ǫ)>0) ou d’un faible gain (Im(∆ǫ)<0, diodes laser DBR ou
DFB).
3

Dans sa forme la plus courante que nous reprenons ici 1, la théorie des modes
couplés est basée sur trois approximations principales :
1. L’approximation du guidage faible qui permet de considérer une équation de
propagation scalaire.
2. On cherche une solution du problème perturbé en fonction des modes du guide
d’onde non-perturbé (traitement perturbatif).
3. L’approximation de l’enveloppe lentement variable qui permet de réduire l’équa-
tion de propagation à une équation différentielle du premier ordre.
La première approximation concerne à la fois le système perturbé et le système non-
perturbé. Les approximations 2 et 3 se justifient par le fait que la modification ∆ǫ
est une perturbation, ∆ǫ≪¯ǫ.
2 Equation de propagation
Dans des milieux non-magnétiques et non-dispersifs caractérisés par une per-
mittivité diélectrique ǫ(x, y, z) = ǫ0n2(x, y, z), avec ǫ0la permittivité du vide et n
l’indice de réfraction, l’équation de propagation du champ électrique s’écrit
∇2E−µ0ǫ∂2E
∂t2− ∇(∇ · E) = 0.(2)
Cette équation se déduit directement des équations de Maxwell 2. Dans toute la suite,
on considère des champs monochromatiques définis par E(r, t) = Re[E(r)e−iωt] =
1
2E(r)e−iωt +c.c., où E(r) est l’amplitude complexe du champ et l’abréviation c.c.
signifie complexe conjugué. L’équation de propagation devient
∇2E+ω2µ0ǫE− ∇(∇ · E) = 0.(3)
Dans le cas général, l’équation de propagation est une équation différentielle vec-
torielle qui couple les trois composantes du champ électrique à cause du troisième
terme ∇(∇ · E). En effet, la divergence du champ électrique n’est pas nulle dans
un milieu inhomogène. C’est la divergence du déplacement électrique D=ǫEqui
est nulle, ∇ · D= 0. En utilisant l’identité ∇ · (ǫE) = ǫ∇ · E+E· ∇ǫ, on obtient
∇ · E=−E·1
ǫ∇ǫ=−E· ∇ ln ǫ.
Dans le cadre de l’approximation du guidage faible, basée sur le fait que les
variations de permittivité qui forment le guide d’onde sont faibles (∇ǫ≪ǫ), on
néglige la divergence du champ électrique, ∇ · E≈0, et l’équation de propagation
devient simplement
∇2E+ω2µ0ǫE= 0.(4)
Cette équation de propagation approchée est maintenant scalaire, c’est-à-dire que
les trois composantes de Evérifient indépendamment la même équation différentielle
1. Voir notamment A. Yariv and P. Yeh, Optical Waves in Crystals, Chaps. 6.4 et 11 (John
Wiley, New York, 1984).
2. ∇ × (∇ × E) = ∇(∇ · E)− ∇2E= [...]
4

(sauf si le tenseur permittivité n’est pas diagonal). Il est intéressant de noter que
dans le cas particulier d’un guide d’onde planaire caractérisé par ǫ(x), les ondes
TE vérifient exactement ∇ · E= 0 puisque dans ce cas les vecteurs Eet ∇ǫsont
perpendiculaires et E· ∇ǫ= 0.
Dans toute la suite de ce Chapitre, on se place dans le cadre de l’approximation
du guidage faible et on considère donc l’équation de propagation donnée par (4).
C’est cette équation que l’on se propose de résoudre dans le cas où la permittivité
ǫpeut s’écrire comme la somme d’une permittivité ¯ǫqui correspond à un guide
d’ondes connu et d’une perturbation ∆ǫ.
3 Expression de la solution du problème perturbé
en fonction des modes du guide non-perturbé
En utilisant l’équation (1), l’équation de propagation dans le guide d’onde per-
turbé peut être réécrite sous la forme suivante
∇2E+ω2µ0¯ǫE=−ω2µ0∆ǫE.(5)
Sous cette forme, on reconnaît l’équation de propagation dans le guide non-perturbé
¯ǫen présence d’un terme source −ω2µ0∆ǫEproportionnel à la perturbation ∆ǫ.
La perturbation peut donc être vue comme une source dont le rayonnement crée le
champ perturbé. Mais attention, il est important d’être conscient du fait que le terme
source est inconnu puisqu’il est proportionnel au champ Erecherché. L’équation (5)
est simplement une réécriture de l’équation de propagation dans le milieu perturbé
qui permet de comprendre physiquement le rôle de la perturbation.
Dans une section non-perturbée du guide, tout champ E0peut être décomposé
sur les modes Em, qui sont les modes propres du guide non-perturbé et qui forment
une base complète, E0=PmAmem(x, y)eiβmz. A cause de la perturbation ∆ǫ, les
modes du guide non-perturbés ne sont plus les modes propres du guide perturbé
et la forme générale E0ne peut pas être utilisée pour exprimer les solutions de
l’équation de propagation dans une section perturbée du guide. Néanmoins, comme
la modification ∆ǫest une perturbation, nous considérerons que le champ Edans
le milieu perturbé est peu modifié et qu’il peut être approché par une expression
semblable à E0faisant intervenir les modes du guide non-perturbé.
Pour comprendre intuitivement comment la présence de la perturbation ∆ǫmo-
difie la décomposition modale donnée par E0, considérons un guide non-perturbé
qui supporte 2 modes E1et E2. Si l’on éclaire avec le mode E1une perturbation
d’épaisseur infinitésimale en z, la présence du ∆ǫcrée une polarisation de pertur-
bation ∆P= ∆ǫE1. Cette polarisation rayonne le mode E1avec une amplitude
modifiée mais également le mode E2. Ainsi, on comprend qu’une perturbation ∆ǫ
couple les modes du guide non-perturbé et permet un échange d’énergie entre eux.
Cet échange d’énergie se traduit par le fait que les amplitudes des modes varient au
cours de la propagation.
Ainsi, l’hypothèse de base de la théorie des modes couplés est la suivante. On
considère que le champ dans le milieu perturbé reste une superposition des modes
5