Mécanique des fluides Viscosité des fluides - Plate

PC* Lyc´ee Hoche M´ecanique des fluides Pascale Piquemal 08/12
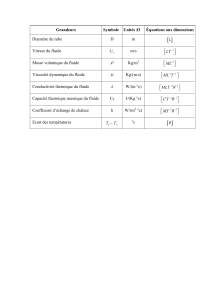
Viscosit´e des fluides
Table 1 – Viscosit´es dynamique et cin´ematique
ηen Pl µen kg.m−3νen m2.s−1
eau 10−310310−6
air 1,8 10−51,3 1,5 10−5
huile d’olive '0,1 9 10210−4
miel '10 1,4 1037 10−3
sang 4 10−31034 10−6
La viscosit´e cin´ematique d’un gaz est du mˆeme ordre de grandeur que son coefficient
d’autodiffusion D et que sa diffusivit´e thermique Dth.
Sujet 1 : Chute d’une bille dans la glyc´erine
Bille de rayon r= 1 cm, pour la glyc´erine η= 1,49 P l et µ= 1,26 103kg.m−3. Evaluer la vitesse
limite de la bille, calculer le nombre de Reynolds et v´erifier la validit´e du calcul.
Sujet 2 : Frottement fluide sur une plaque en mouvement rectiligne uniforme
Un fluide incompressible ( masse volumique µ, viscosit´e dynamique η,η
µ=ν= 10−6m2s−1) est limit´e
par deux plaques suppos´ees infinies, confondues avec les plans d’´equation z= 0 et z=L. Le fluide
et les deux plaques ´etant au repos `a t < 0, on met en mouvement la plaque z= 0 avec une vitesse
constante U−→ ux`a partir de t= 0. On note P(z, t)le champ de pression et −−−−→ v(M, t) = v(z, t)−→ uxle champ
des vitesses dans le fluide.
1/ En isolant un pav´e de cˆot´es dx, dy et dz, ´etablir les relations : ∂v
∂t =ν∂2v
∂z2et dP
dz =−µg.
2/ Pr´evoir sans calcul l’ordre de grandeur de la dur´ee τd’´etablissement d’un ´ecoulement stationnaire.
A.N : L= 1 cm et L= 1 m.
3/ On se place en r´egime stationnaire. D´eterminer v(z) et la force subie par un ´el´ement de surface de
la plaque mobile. Commenter.
Sujet 3 : Freinage d’une plaque en mouvement sinuso
¨
ıdal. Ondes de cisaillement dans un
fluide
Une plaque confondue avec le plan d’´equation z=0 est en translation avec une vitesse Ucos(ωt)−→ ux
dans un fluide incompressible ( masse volumique µ, viscosit´e dynamique η,η
µ=ν= 10−6m2s−1)
remplissant tout l’espace. On note P(z, t)le champ de pression et −−−−→ v(M, t) = v(z, t)−→ uxle champ des
vitesses dans le fluide.
1/ En isolant un pav´e de cˆot´es dx, dy et dz, ´etablir les relations : ∂v
∂t =ν∂2v
∂z2et dP
dz =−µg. En d´eduire
sans calculs l’ordre de grandeur de l’´epaisseur δde la couche limite, domaine hors duquel le fluide reste
quasiment au repos. A.N : f= 100 Hz.
2/ On cherche en r´egime sinuso¨ ıdal forc´e un champ de vitesses de la forme v(z, t) = <(UMexpj(ωt−kz))
. D´eterminer k et en d´eduire les expressions de v(z > 0, t)et v(z < 0, t).
3/ En d´eduire l’expression de la force subie par l’unit´e de surface de la plaque et la puissance de cette
force ; commenter.
Sujet 4 : Ecoulement d’un liquide sur un plan inclin´e
Consid´erons une couche, d’´epaisseur h, d’un liquide incompressible visqueux, de viscosit´e ηet de masse
volumique µ, en ´ecoulement sur un plan inclin´e faisant avec l’horizontale un angle αet on note la ligne
de plus grande pente Ox dirig´ee vers le bas . En ´ecoulement stationnaire, celui-ci est unidirectionnel et
1

PC* Lyc´ee Hoche M´ecanique des fluides Pascale Piquemal 08/12
la seule composante non nulle de la vitesse v ne d´epend que de z, soit vx(z). La surface libre correspond
`a z= 0 et le plan supportant la couche `a z=h.
1/ Justifier que ∂P
∂x = 0.
Ox
Oz
Figure 1 – Ecoulement
d’un liquide sur un plan in-
clin´e
2/ D´eterminer les conditions limites en termes de vitesse en n´egligeant
la viscosit´e de l’air.
3/ En d´eduire le profil de vitesse d’un tel ´ecoulement. Identifier le type
d’´ecoulement observ´e en fonction de α.
4/ La couche de liquide est de largeur L dans la direction Oy. Cette lar-
geur est tr`es grande devant la profondeur h. Calculer le d´ebit volumique
et en d´eduire la vitesse moyenne de l’´ecoulement. Pourquoi ce d´ebit est-il
constant ?
5/ A.N : calculer la vitesse moyenne de l’´ecoulement pour une rivi`ere de h= 1 mpr´esentant une
diff´erence d’altitude de 50 mapr`es un parcours de 500 km. Ce r´esultat est-il r´ealiste ? puis pour une
couche d’eau de h= 2 mm sur un plan inclin´e de 1◦par rapport `a l’horizontale.
R´eponses partielles : Conditions limites, penser `a l’annulation de la contrainte tangentielle en z= 0.
v(z) = µg sin α(h2−z2)
2η. C’est irr´ealiste pour la rivi`ere car ´ecoulement parfait sauf dans la couche limite.
En revanche pour la couche d’eau, tout l’´ecoulement est visqueux.
Sujet 5 : Ecoulement de Navier-Stokes entre deux cylindres de r´evolution coaxiaux
On consid`ere deux cylindres de r´evolution coaxiaux, d’axe Oz, de rayons R1et R2avec R1< R2.
On ´etudie un ´ecoulement stationnaire, longitudinal, d’un fluide visqueux de viscosit´e dynamique η,
incompressible, de masse volumique µ. La perte de charge sur une longueur L de conduite est not´ee
∆p=p(z= 0) −p(z=L).
1/ D´emontrer que v ne d´epend que de r en coordonn´ees cylindriques d’axe Oz.
2/ D´emontrer que p est fonction lin´eaire de la seule variable z.
3/ En d´eduire le champ des vitesses v(r) en fonction de la perte de charge par unit´e de longueur ∆p/L.
4/ Calculer le d´ebit massique le long de la conduite.
5/ Comment peut-on reformuler le probl`eme si l’on n´eglige la viscosit´e ? R´eponse partielle : v(z) =
−∆P r2
4Lη +clnr +c0.
Sujet 6 : Ecoulement de Poiseuille cylindrique
Un tel ´ecoulement, dit de Poiseuille, correspond `a celui d’un liquide visqueux (de viscosit´e ηet de
masse volumique µ) dans une conduite cylindrique de rayon Ret d’axe Oz. On n´eglige les effets de la
pesanteur.
1/ Du fait des sym´etries du probl`eme, on cherche en coordonn´ees cylindriques un champ de la forme
−→
v=v(r, z)−→ uzet un champ de pression de la forme P(M) = p(r, z). L’´ecoulement est stationnaire et
incompressible. Exploiter l’incompressiblilit´e de l’´ecoulement. Appliquer le th´eor`eme de la r´esultante
cin´etique `a une particule de fluide.
2/ En d´eduire le champ des vitesses en tenant compte des conditions aux limites sur la paroi de la
conduite. En d´eduire l’expression du d´ebit volumique en fonction des pressions `a l’entr´ee et `a la sortie
pour une conduite de longueur L. Comparer `a la loi d’Ohm pour un conducteur filiforme.
3/ A.N : Calculer la chute de pression dans une art`ere de longueur L= 1 m, de rayon R= 0,5cm et
de d´ebit volumique 80 cm3s−1, sachant que la viscosit´e du sang vaut η= 4 10−3P l. Comparer avec la
diff´erence de pression que maintient le coeur ? p= (12 −8) cm = 4 cm de mercure.
R´eponses : v(z) = ∆P(R2−r2)
4Lη et Dv=∆P πR4 8Lη .
2