1. Analyse d`une carte météorologique

1
MASTER 1ET MAGIST ` ERE 2DE
PHYSIQUE FONDAMENTALE
...........................................................................................
M´ ECANIQUE DES FLUIDES (M1PHYSF-404A-A)
EXAMEN DU MARDI 9NOVEMBRE 2010
(Dur´ ee : 3 heures - sans document)
...........................................................................................
1. Analyse d’une carte m´ et´ eorologique
Les grandes circulations atmosph´ eriques sont domin´ ees par l’effet de la rotation de la Terre ainsi
que par la stratification en densit´ e de l’air. Dans ce probl` eme, on consid` ere toutefois l’atmosph` ere
comme isodensit´ e pour simplifier, et l’on s’int´ eresse seulement ` a l’influence de la rotation de la Terre
sur la structure des ´ ecoulements.
On admet que, dans un r´ ef´ erentiel tournant de vecteur instantan´ e de rotation ~ Ω, l’´ equation de
Navier-Stokes pour un fluide isodensit´ e, s’´ ecrit :
∂~u
∂t + (~u ·~
∇)~u =−1
ρ~
∇p−2~ Ω∧~u +ν~ ∇2~u, (1)
o` u~u est la vitesse relative du fluide dans le r´ ef´ erentiel tournant. Le terme suppl´ ementaire −2~ Ω∧~u est
la force de Coriolis (par unit´ e de masse). La force centrifuge et la force de gravit´ e n’apparaissent pas,
car elles sont incluses dans le terme de pression modifi´ ee p: elles n’interviennent donc pas dans la
suite.
On consid` ere un rep` ere local Cart´ esien, tel que (x, y)est tangeant ` a la surface de la Terre et
zselon la verticale locale. Pour simplifier, nous allons nous restreindre ` a l’´ etude d’´ ecoulements at-
mosph` eriques au voisinage du pˆ ole Nord : on peut alors prendre ~ Ω=Ω~ez, avec Ω>0et ~ezl’axe de
rotation de la Terre. On note Lla taille caract´ eristique des structures de l’´ ecoulement, Uleur vitesse
caract´ eristique, et T=L/U le temps caract´ eristique d’´ evolution du champ de vitesse.
1. D´ eterminer les ordres de grandeur des termes inertiels, visqueux et de Coriolis de l’´ equation
(1). Dans le cadre de l’approximation g´ eostrophique, cette ´ equation devient
~
∇p=−2ρ~ Ω∧~u. (2)
Exprimer, en fonction des nombres de Reynolds Re =UL/ν et de Rossby Ro =U/2ΩL, les
conditions sous lesquelles cette approximation est v´ erifi´ ee. En d´ eduire que le vecteur vitesse est
alors dirig´ e le long des isobares (c’est-` a-dire perpendiculaire ` a~ ∇p).
2. Calculer la vitesse angulaire Ωde la Terre, et en d´ eduire le nombre de Rossby dans le cas
d’une d´ epression (10 m/s sur 400 km), d’une tornade (20 m/s sur 20 m) et de la vidange d’une
baignoire. Qu’en d´ eduisez-vous de l’influence de la rotation de la Terre sur ces 3 ´ ecoulements ?

2
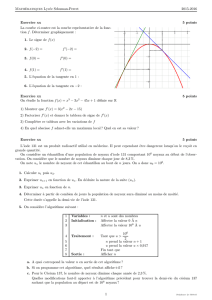
1100 km
FIGURE 1 – Champ de pression. Les isobares sont espac´ ees de 400 Pa. Les centres de haute et
basse pression sont not´ es H(high) et L(low). Les lignes marqu´ ees de triangles ou de demi-cercles
repr´ esentent respectivement les fronts froids et chauds.
3. Ecrire les projections de l’´ equation (2) selon les 3 axes des coordonn´ ees cart´ esiennes (on notera
~u =ux~ex+uy~ey+uz~ezles composantes de la vitesses). A partir du rotationnel de l’´ equation
(2), en d´ eduire que :
(i) l’´ ecoulement horizontal (ux, uy)satisfait une condition d’incompressibilit´ e bi-dimensionnelle.
(ii) le champ de vitesse ~u est invariant par translation selon z(ce r´ esultat porte le nom de
th´ eor` eme de Taylor-Proudman).
4. En tenant compte des conditions aux limites en z= 0, en d´ eduire que le champ de vitesse est
horizontal (2D2C) en tout point.
5. A partir d’une ´ evaluation du gradient de pression, estimez la vitesse du vent au voisinage de
la grande zone d´ epressionnaire situ´ ee sur l’Ecosse sur la carte de la figure 1 (au centre de la
carte). On prendra ρ= 0.6kg m−3pour la densit´ e moyenne de l’air en altitude). Commenter
ce r´ esultat. Que pensez-vous du nombre de Rossby dans cette r´ egion ?
6. Montrer que le Laplacien de la pression s’´ ecrit
∇2p= 2ρΩωz,(3)
o` uωzest la composante selon zde la vorticit´ e~ω =~ ∇∧~u.

3
7. On consid` ere un grand tourbillon de sym´ etrie circulaire : il s’agit par convention d’un cy-
clone s’il tourne dans le mˆ eme sens que la Terre, et d’un anticyclone dans le cas contraire.
En consid´ erant que l’on a ωz=cste pr` es du centre du tourbillon (approximation de rota-
tion solide), en d´ eduire le champ de pression p(r)dans ce grand tourbillon, par int´ egration
de l’´ equation (3) en coordonn´ ees cylindriques (r, θ, z). Le Laplacien dans ces coordonn´ ees est
donn´ e par
∇2f=1
r
∂
∂r r∂ ∂r f+1 r2
∂2
∂θ2f+∂2 ∂z2f.
8. En d´ eduire l’´ equivalence suivante :
- cyclone →d´ epression ;
- anticyclone →surpression.
Peut-on v´ erifier cette ´ equivalence sur la figure 1 ? Cette ´ equivalence est-elle toujours vraie au
pˆ ole Sud ?
9. Les frottements avec la surface de la Terre font que l’´ equilibre g´ eostrophique (2) n’est plus
v´ erifi´ e` a basse altitude. Il existe une couche limite, d’´ epaisseur not´ ee δ, de plusieurs centaines
de m` etres, telle que pour zδl’´ equation (2) reste valide, tandis que pour zδc’est le terme
ν∂2
∂z2~u qui ´
equilibre le gradient de pression.
a) Si l’on consid` ere l’´ ecoulement comme strictement horizontal ` a toute altitude, montrer que
la pression reste partout ind´ ependante de z.
b) On admettra qu’` a basse altitude le vecteur vitesse est maintenant align´ e avec le gradient
de pression. Dans le cas d’un anticyclone (respectivement une d´ epression), d´ eduire de la
question 6 qu’il doit exister une vitesse radiale sortante (respectivement rentrante) pr` es de
la surface de la Terre.
c) Montrer qu’il existe ´ egalement alors une petite vitesse verticale dans le tourbillon, et com-
menter son signe.
d) Il est bien connu que la pr´ esence d’un anticyclone favorise un temps sec, tandis qu’une
d´ epression est souvent associ´ ee ` a un temps pluvieux. Pouvez-vous interpr´ eter ces ph´ eno-
m` enes ?

4
2. Effet Marangoni
La tension interfaciale, par exemple entre un liquide et un gaz est g´ en´ eralement une fonction
d´ ecroissante de la temp´ erature γ(T). Nous allons ´ etudier un syst` eme qui permet de mesurer cette
d´ ependance.
On place une mince couche de liquide d’´ epaisseur de l’ordre de h0dans un r´ ecipient rectangulaire
horizontal (voir figure 2). On notera γla tension de surface et γ0=dγ
dT sa d´
ependance en temp´ erature
que l’on supposera constante et n´ egative dans la gamme d’´ etude (γ0<0). On notera ηet ρla viscosit´ e
dynamique et la masse volumique du liquide.
On impose un gradient de temp´ erature G=dT
dx uniforme et constant (G < 0) entre la gauche et
la droite du r´ ecipient. On n´ egligera la variation de la masse volumique du liquide avec la temp´ erature
(qui conduirait ` a de la convection thermique classique).
0
z
x
C
haud Froid
h ( x )
Air
Liquide
FIGURE 2 – Fine couche de liquide plac´ ee dans un gradient horizontal de temp´ erature T(x).
1. Ecrire la force de tension interfaciale d~ Fγqui s’exerce de chaque cˆ ot´ e d’une ligne de longueur
dl de l’interface gaz/liquide en fonction de γet de dl. Quelle est la dimension de γ?
2. Ecrire la d´ ependance T(x)de la temp´ erature. On notera T0la temp´ erature en x= 0. En d´ eduire
la variation spatiale γ(x)de la tension de surface.
3. Montrer qu’une portion de surface comprise entre xet x+dx et de dimension transverse L
selon Oy est soumis ` a une diff´ erence de forces de tension de surface d~ Fγ, que l’on repr´ esentera
et que l’on calculera.
4. A partir du bilan de force pr´ ec´ edent, montrer qualitativement que la d´ ependance en temp´ erature
de la tension de surface conduit ` a un mouvement du liquide en surface. Dans quel direction se
fait ce mouvement de surface ? Tracer l’allure de l’´ ecoulement dans l’´ epaisseur de la couche en
r´ egime permanent.
Dans la suite nous allons quantifier ce ph´ enom` ene et montrer qu’il conduit en r´ egime permanent
`
a une inclinaison de la surface du liquide d’un angle θque l’on va calculer. Nous supposerons
que cet angle reste toujours faible (h(x)≈h0), et que le r´ ecipient est long afin de pouvoir
n´ egliger les effets de bords.
5. En consid´ erant la viscosit´ e du liquide (on n´ egligera la viscosit´ e de l’air) ´ ecrire la contrainte vis-
queuse σ0
xz exerc´
ee par la surface mobile sur le fluide. A-t-on une surface libre stricto sensu ?

5
En appliquant le principe fondamental de la dynamique ` a cette surface, en d´ eduire la relation
entre γ0et ∂u
∂z hqui existe en r´
egime permanent, o` uuest la composante horizontale de la
vitesse selon Ox.
6. Ecrire l’´ equation de Navier-Stokes en r´ egime permanent selon les directions horizontale et ver-
ticale. On supposera v´ erifi´ ees les approximations de la lubrification (´ ecoulement faiblement
non-parall` ele). Montrer que dans ce cas, on trouve une relation simple entre ∂p
∂x et ∂2u ∂z2.
7. Par int´ egration selon Oz trouver la pression p(x, z)en tout point du fluide. On notera Patm la
pression dans l’air. En particulier montrer qu’en r´ egime permanent ∂p
∂x est reli´
e` a∂h
∂x = tan θ(x)
(on prendra tan θ'θ).
8. Par int´ egration et en appliquant la condition au limite ` a la surface trouv´ ee en 5, calculer la fonc-
tion u(z).
9. Calculer le d´ ebit volumique Qv(x)` a travers une section verticale d’abscisse xquelconque. Que
vaut ce d´ ebit en r´ egime permanent ? En d´ eduire une relation lin´ eaire entre γ0et θsi h(x)≈h0.
Le r´ esultat d´ epend-il de la viscosit´ e du liquide ?
10. Tracer le profil de vitesse u(x, z)` axfix´ e pour z∈[0, h(x)].
11. A.N. : On donne G=−10 K/m, ρ= 860 kg/m3,h0= 3 mm et θ= 1◦. Calculer γ0. Si le
liquide est de l’huile, η= 0.1Pa s, calculer la vitesse du liquide en surface. L’approximation
d’´ ecoulement de lubrification ´ etait-elle bien justifi´ ee ?
12. D´ ecrire une ou plusieurs m´ ethodes permettant de mesurer θavec pr´ ecision.