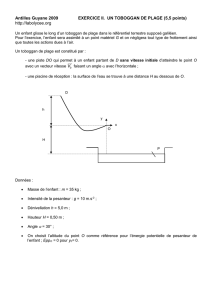
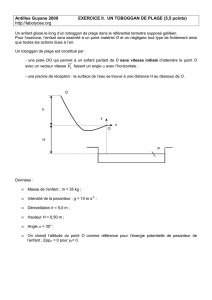
Me111 - Mécanique générale Faïz Ben Amar

Université de Versailles StQuentin
UFR des Sciences et Technologies
Licence SPI
Me111 - Mécanique générale
Faïz Ben Amar
[e-mail]

Chapitre 1
Introduction
1.1 Quelques définitions et terminologie
La mécanique générale a pour but l’étude des mouvements des corps dans l’univers. La
mécanique classique se décompose en :
– la cinématique : c’est l’étude des mouvements faisant intervenir des grandeurs ne dé-
pendant que du temps et de l’espace
– la cinétique : c’est l’étude des mouvements en intégrant en plus les masses et leurs
répartitions,
– la dynamique : c’est l’étude des mouvements des corps en tenant compte des forces qui
s’exercent sur ces corps,
1.1.1 Notion de solide rigide ou indéformable
Une pièce mécanique (S) peut être considérée comme un solide indéformable si quels que
soient les points Aet Bde (S), la distance AB reste constante au cours du temps t.
1.1.2 Notion de référentiel
La notion de mouvement d’un point ou d’un corps est tout à fait relative. On parle du
mouvement de la lune par rapport à la terre, du mouvement d’une voiture par rapport
à la chaussée, ... Décrire un mouvement donc n’a de sens que si on choisi un solide de
référence auquel on associe un repère appelé référentiel.
Exemple : on définit un repère R0= (O,~ i0,~ j0,~ k0)lié au socle (S0)et fixe par rapport au
sol pour définir le mouvement d’un robot.
1.1.3 Mesure du temps
La notion d’écoulement du temps de manière régulière et irréversible est donnée à l’ob-
servateur par des mouvements particuliers appelés horloge (pendule, quartz, horloge ato-
mique...)
1.2 Grandeurs vectorielles de la cinématique
Soit R0= (O,~ i0,~ j0,~ k0)un repère orthonormé direct. Soit (S) un solide en mouvement
par rapport à R0.
2

1.2.1 Vecteur position
On appelle vecteur position du point Pquelconque du solide (S) dans le repère R0, à la
date t, le vecteur −→ OP où Oest l’origine du repère R0.
Le point P appartenant au solide (S) est appelé point matériel de (S). Ce point matériel
coincident à chaque instant avec un point géométrique du repère R0. L’ensemble de ces
points géométriques est une courbe (C) qui constitue la trajectoire de P dans le repère
R0.
−→
O0P(t) = x(t)
~
i0+y(t)~ j0+z(t)~ k0
x=x(t)
y=y(t)
z=z(t)
sont les équations paramétriques de la trajectoire de Pdans R0.
1.2.2 Vecteur vitesse
Le vecteur vitesse d’un point Ppar rapport à R0, à la date t, est la dérivée par rapport
au temps, pour un observateur lié au repère R0, du vecteur position du point Pdans R0.
−→
V(P/R0) = "d−→
O0P
dt #R0
−→
V(P/R0) = "d−→
O0P(t)
dt #R0
=
dx(t)
~
i0+y(t)~ j0+z(t)~ k0
dt 
R0
=dx
dt~
i0+dy
dt~
j0+dz
dt~
k0
= ˙x
~
i0+ ˙y~ j0+ ˙z~ k0
Remarque :
– unité : m/s ou m.s−1
– on peut préciser −→
V(P, S/R0), s’il s’agit d’un point matériel de (S).
– il n’est pas nécessaire d’exprimer ce vecteur dans la base de R0d’observation de la
vitesse.
– pour pouvoir calculer correctement cette dérivée, il est important de préciser le repère
de dérivation.
1.2.3 Vecteur Accélération
Le vecteur accélération d’un point Ppar rapport à R0, à la date t, est la dérivée par
rapport au temps, pour un observateur lié au repère R0, du vecteur vitesse du point P
par rapport à R0.
F. Ben Amar UVSQ - Licence SPI - Me111 - Introduction - Torseur 3

−→
γ(P/R0) = "d−→
V(P/R0)
dt #R0
="d2−→
O0P
dt2#R0
−→
γ(P/R0) = 
d˙x
~
i0+ ˙y~ j0+ ˙z~ k0
dt 
R0
= ¨x
~
i0+ ¨y~ j0+ ¨z~ k0
Remarque :
– unité : m/s2ou m.s−2
– il n’est pas non plus nécessaire d’exprimer ce vecteur accélération dans la base de R0.
1.3 Torseur
1.3.1 Définition mathématique
Un torseur {T } est un bi-vecteurs (~ R, ~ MP), noté
{T } =(−→
R
−→
MP)P
où :
–−→
R: vecteur constant appelé résultante,
–−→
MP: appélé moment en P, vecteur champ, dépendant du point, et qui doit satisfaire
la relation suivante, dite de transport ou de changement de point,
−→
MA=−→ MB+−→
AB ∧−→
R
1.3.2 Propriétés
– L’équiprojectivité du champ de moment :
−→
MA.−→
AB=−→
MB.−→
AB ∀A, B
– L’invariant scalaire d’un torseur :
I=−→
R.−→ MA=−→ R.−→ MB
– L’axe central et le pas d’un torseur : L’axe central est l’ensemble des points Ptel que
−→
MP=λ−→ R
F. Ben Amar UVSQ - Licence SPI - Me111 - Introduction - Torseur 4

où λest un scalaire appelé le pas. On montre que λest unique et vaut
λ=
−→
R.−→ MA
−→
R
2
On montre également que l’axe est une droite affine de vecteur directeur −→
Ret passe
par le point Htel que
−→
AH=
−→
R∧−→ MA
−→
R
2
L’amplitude du moment sur l’axe du torseur est minimal.
1.3.3 Quelques torseurs particuliers
– Le torseur nul : si −→
R=−→
0et −→
MP=−→
0,
– Le glisseur : si −→
MA.−→ R= 0 ou l’invariant scalaire nul. Le moment d’un glisseur est
orthogonal à la résultante. L’invariant et le pas sont nuls. Le moment sur l’axe est nul.
– Le torseur couple : si −→
R=−→
0et −→
MP6=−→
0. Le moment d’un torseur couple est invariant.
1.3.4 Torseur d’effort
Ce torseur, dit aussi torseur statique, permet de caractériser toute action mécanique, en
la réduisant à deux vecteurs, noté :
{F} =(−→
R
−→
MA)A
Si cette action mécanique est une action de contact, c’est-à-dire surfacique, de densité
surfacique
−→
fs(P) =
−→
df
ds
{F} =(−→
R=RRS
−→
fs(P)ds
−→
MA=RRS
−→
AP ∧
−→
fs(P)ds )A
Si cette action mécanique est une action à distance, c’est-à-dire volumique, de densité
volumiqe
−→
fv(P) =
−→
df
dv
{F} =(−→
R=RRRV
−→
fv(P)dv
−→
MA=RRS
−→
AP ∧
−→
fv(P)dv )A
1.3.5 Quelques actions simples
– La force : une force −→
Fs’appliquant au point Ppeut être représentée par un torseur
{F} =(−→
R=−→ F
−→
MA=−→
AP ∧−→
F)A
≡(−→
R=−→ F
−→
MA=−→
0)P
Ce torseur est de type glisseur. La propriété des glisseurs vient du fait que si la résultante
(force) glisse sur son support, l’action mécanique est statiquement équivalente.
F. Ben Amar UVSQ - Licence SPI - Me111 - Introduction - Torseur 5