EXOS-BAC 02 : Continuité et convexité Exercice

TES
6 novembre 2015
EXOS-BAC 02 : Continuité et convexité
Exercice 1
On considère la fonction fdéfinie sur l’intervalle [2 ; 8] par : f(x)=
−x2+10x−16
x2
On appelle Csa courbe représentative dans un repère.
1. Montrer que pour tout réel de l’intervalle [2 ; 8], on a : f′(x)=
−10x+32
x3
2. a. Étudier le signe de f′(x) sur l’intervalle [2 ; 8].
b. En déduire le tableau de variations de fsur l’intervalle [2;8].
3. On appelle f′′ la dérivée seconde de fsur [2 ; 8].
On admet que, pour tout réel xde l’intervalle [2 ; 8], on a : f′′(x)=20x−96
x4
a. Montrer que fest une fonction convexe sur [4,8 ; 8].
b. Montrer que le point de (C) d’abscisse 4,8 est un point d’inflexion.
Exercice 2
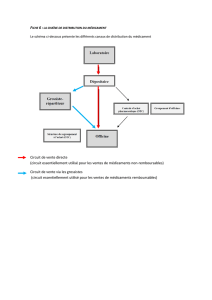
Un laboratoire pharmaceutique fabrique un médicament qu’il commercialise sous forme liquide. Sa capacité
journalière de production est comprise entre 0 et 500 litres, et on suppose que toute la production est commer-
cialisée.
Dans tout l’exercice, les coûts et recettes sont exprimés en milliers d’euros, les quantités en centaines de litres.
Si xdésigne la quantité journalière produite, on
appelle CT(x), pour xvariant de 0 à 5, le coût total de
production correspondant.
On sait que CT(x)=0,15(x−1)3+1 et que cette
fonction a pour représentation graphique sur l’inter-
valle [0;5] la courbe C.
La tangente à Cau point A(1;1) est horizontale.
−2−1 1 2 3 4 5
1
2
3
4
5
6
7
8
9
0
C
A
x en cent ai nes
d e l i t r e s
Coût tot al
d e pr oduc t i on
∀T ES Page 1/2 Tournez, SVP !

PARTIE A
1. On admet que la recette R(x) (en milliers d’euros) résultant de la vente de xcentaines de litres de médica-
ment, est définie sur [0 ; 5] par R(x)=1,5x.
a. Quelle est la recette (en euros) pour 200 litres de médicament vendus ?
b. Tracer, sur le graphique donné ci-dessus, le segment représentant graphiquement la fonction R.
2. Lectures graphiques
Les questions a., b., c. suivantes seront résolues à l’aide de lectures graphiques seulement. On fera apparaître
les traits de construction sur le graphique.
Toute trace de recherche même non aboutie sera prise en compte.
a. Déterminer des valeurs approximatives des bornes de la « plage de rentabilité », c’est-à-dire de l’inter-
valle correspondant aux quantités commercialisées dégageant un bénéfice positif.
b. Donner une valeur approximative du bénéfice en euros réalisé par le laboratoire lorsque 200 litres de
médicament sont commercialisés.
c. Pour quelle quantité de médicament commercialisée le bénéfice paraît-il maximal ?
À combien peut-on évaluer le bénéfice maximal obtenu ?
PARTIE B
1. Justifier que le bénéfice, en milliers d’euros, réalisé par le laboratoire pour xcentaines de litres commercia-
lisés, est donné par :
B(x)= −0,15x3+0,45x2+1,05x−0,85
Calculer B(2), et comparer au résultat obtenu à la question 2.b de la partie A.
2. On suppose que le fonction Best dérivable sur l’intervalle [0 ; 5] et on note B′sa fonction dérivée.
Calculer B′(x).
3. Dresser le tableau de variations de la fonction Bsur l’intervalle [0 ; 5] .
4. a. Pour quelle quantité de médicament commercialisée, le bénéfice est-il maximal ? (on donnera une
valeur approchée en litres).
Donner alors une valeur approchée en euros de ce bénéfice maximal.
b. Ces résultats sont-ils cohérents avec ceux obtenus graphiquement à la question 2.c de la partie A.
5. Calculer B′′(x). Montrer que la courbe admet un point d’inflexion. En donner une interprétation écono-
mique.
∀T ES Page 2/2 Fin