Réinvestir en économie : correction

TES AP n°4 : Corrigé
1
TES AP n°4 : Corrigé
Exercice 1
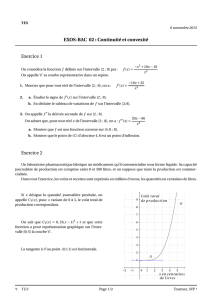
Un laboratoire pharmaceutique fabrique un médicament qu’il commercialise sous forme liquide.
Sa capacité journalière de production est comprise entre 0 et 500 litres, et on suppose que toute la
production est commercialisée.
Dans tout l’exercice, les coûts et recettes sont exprimés en milliers d’euros, les quantités en centaines de
litres.
Si x désigne la quantité journalière produite, on appelle
T
Cx
, pour x variant de 0 à 5, le coût total de
production correspondant.
La courbe fournie en annexe est la représentation graphique de la fonction
T
C
sur l’intervalle
0;5
.
Partie A
On admet que la recette
Rx
( en milliers d’euros ) résultant de la vente de x centaines de litres de
médicament, est définie sur
0;5
par
1,5R x x
.
1. a. Quelle est la recette ( en euros ) pour 200 litres de médicament vendus ?
2 1,5 2 3R  
donc la recette pour 200 litres de médicament vendu est de 3 000 €.
b. Sur le graphique en annexe, tracer le segment représentant graphiquement la fonction R.
2. Lectures graphiques
Les questions a.,b. et c. suivantes seront résolues à l’aide de lectures graphiques seulement. On fera
apparaître les traits de construction sur le graphique.
Toute trace de recherche même non aboutie sera prise en compte.
a. Déterminer des valeurs approximatives des bornes de la « plage de rentabilité », c'est-à-dire de
l’intervalle correspondant aux quantités commercialisées dégageant un bénéfice positif.
Le bénéfice est positif quand la recette est supérieure au coût. Graphiquement, sur l’intervalle I ]0,7 ;4,3[,
la courbe représentative de R se situe au dessus de la courbe .
Donc quand l’entreprise commercialise entre 70 litres et 430 litres de médicament le bénéfice est positif.
b. Donner une valeur approximative du bénéfice, en euros réalisé par le laboratoire lorsque 200 litres de
médicament sont commercialisés.
Le coût total d’une production de 200 litres est d’environ 1 200 € et la recette dégagée par la vente de ces
200 litres est de 3 000 € donc le bénéfice est d’environ 1 800 €.
c. Pour quelle quantité de médicament commercialisée le bénéfice paraît-il maximal ?
A combien peut-on évaluer le bénéfice maximal obtenu ?
Graphiquement on peut estimer que pour x environ égal à 2,8 « l’écart entre les deux courbes » est
maximal.
On lit
2,8 1,9
T
C
et
2,8 1,5 2,8 4,2R  
. Donc
2,8 2,8 2,3
T
RC
.
On peut estimer que si l’entreprise commercialise environ 280 litres de médicament le bénéfice sera
maximal. Ce bénéfice maximal est d’environ 2 300 €.
Partie B
On admet que la fonction coût total
T
C
est définie sur
0;5
par :
32
0,15 0,45 0,45 0,85
T
C x x x x   
.

TES AP n°4 : Corrigé
2
1. Justifier que le bénéfice, en milliers d’euros, réalisé par le laboratoire pour x centaines de litres
commercialisés, est donné par
32
0,15 0,45 1,05 0,85B x x x x    
.
Calculer
2B
et comparer au résultat obtenu à la question 2.b. de la partie A.
Le bénéfice est égal à la recette moins le coût donc, pour tout x de [0 ;5],
3 2 3 2
1,5 0,15 0,45 0,45 0,85 1,5 0,15 0,45 0,45 0,85
T
B x R x C x x x x x x x x x           
Donc
3 2 3 2
0,15 0,45 1,5 0,45 0,85 0,15 0,45 1,05 0,85
T
B x R x C x x x x x x x x            
.
32
2 0,15 2 0,45 2 1,05 2 0,85 1,79B        
.
Dans la partie A on a obtenu
2 1,8B
. Les deux valeurs sont proches.
2. On suppose que la fonction B est dérivable sur l’intervalle
0;5
et on note
'B
sa fonction dérivée.
Calculer
'Bx
.
Pour tout x de [0 ;5],
22
' 0,15 3 0,45 2 1,05 1 0 0,45 0,9 1,05B x x x x x           
3. Dresser le tableau de variation de la fonction B sur l’intervalle
0;5
.
Pour dresser le tableau de variation de B il faut étudier le signe de
'B
.
On commence par étudier le signe du trinôme
2
0,45 0,9 1,05xx  
:
0,45a
0,9b
1,05c
Le discriminant de ce trinôme est
2
0,9 4 0,45 1,05 2,7      
;
0
donc le trinôme admet deux
racines distinctes :
10,9 2,7
2 0,45
x
, soit
12,826x
et
20,9 2,7
2 0,45
x
, soit
20,826x
.
Le coefficient de
2
x
est strictement négatif et
21
xx
, on peut dresser le tableau de signe suivant :
x
2
x
1
x
Signe de
2
0,45 0,9 1,05xx  
0 + 0
On se place maintenant sur l’intervalle [0 ;5] et on dresse le tableau de variation de B :
12,326Bx 
4. a. Pour quelle quantité de médicament commercialisée, le bénéfice est-il maximal ? ( On donnera une
valeur approchée de cette quantité en litres) . Donner alors une valeur approchée en euros de ce bénéfice
maximal.
D’après le tableau de variation précédent, le bénéfice B est maximal pour
12,826x
et a pour valeur
12,326Bx 
.
x
0
1
x
5
Signe de
'Bx
+ 0
Variations
de B
1
Bx
0,85
3,1

TES AP n°4 : Corrigé
3
Donc si l’entreprise commercialise environ 283 litres de médicament le bénéfice est maximal et est environ
égal à 2 826 €.
b. Ces résultats sont-ils cohérents avec ceux obtenus graphiquement à la question 3.c. de la partie A ?
Ces résultats sont cohérents avec ceux obtenus graphiquement dans la partie A.
Annexe
Exercice 2 : Livre n°37 page 54 ( dans la note 2 lire « le coût moyen
M
Cx
…….
MCx
Cx x
. )
Volume du médicament produit
( en centaines de litres )
Coût total ( en milliers d'euros )
2,8 4,3 0,7
1,2
1,9
4,1
2 3 4 5
2
3
4
5
6
7
8
9
10
11
-1
0 1
1