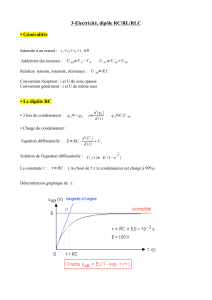
Dipôles linéaires, régime transitoire

I Dipôles R, L, C.
A) Dipôles linéaires
i
u
Un dipôle est dit linéaire lorsque u et i sont liés par une équation différentielle
linéaire à coefficients constants :
n
n
n
n
n
ndt id
b
dt
di
bibC
dtud
a
dt
du
aua ...... 1010
, avec les ai,bi constants.
B) Résistors
1) Dipôle linéaire
Riu
ou
Guu
R
i 1
R
i
u
11 A.V][][][ iuR
(Ohm)
SuiG 11 V.A][][][
(Siemens)
2) Association en série ou en parallèle
Les dipôles sont en série lorsque ils appartiennent à une même branche (il
n’y a pas de nœuds entre eux).
R1R2R3R4Rn
iAB
uAB
u1u2u3u4un
A B
ABjj iRunj ,;1
. On a :
AB
n
jjAB
n
jjuRiu 11
.
On a
n
jjéq
n
jjéq GG
RR 11
11
Les dipôles sont en parallèle lorsqu’ils sont liés à deux mêmes nœuds du
circuit.
R1R2R3R4Rn
iAB A
B
uAB i1i2i3i4in
ABjj uGinj ,;1
.D’après la loi des noeuds :
n
jjAB
n
jjAB Guii 11
Dipôles linéaires, régime transitoire

On a
n
jjéq
n
jjéq RR
GG 11
11
3) Diviseur de tension
R1
R2
i
u
u2
iRRu
iRu
)( 21
22
donc
u
RR R
u
21
2
2
4) Diviseur de courant
i
i1
i2
R1
R2
u
uGGi
uGi
)( 21
22
donc
i
GG G
i
21
2
2
C) Bobines
Bobine idéale :
dt
di
Lu
.L est l’inductance de la bobine, positive.
HΩ.s itu
L
(Henry).
Bobine réelle :
dt
di
Lriu
(i est continu)
La bobine est donc un dipôle linéaire.
D) Condensateur
i i
u
+q
Plaques conductrices de charges
opposées +q et -q
Conservation de la charge :
)ou ( dtttQv
: charge dans v (armature de gauche) à t
ou
dtt
.
dt
dq
dt tqdttq
idtitqdttqdtitQdttQ vv
)()(
)()()()(
oùC
est une constante positive, la capacité du condensateur.
Relation entre u et i :
i
dt
du
C
dt
dq
Cdt
du
C
q
u 1
(doncu est continue)
Le condensateur est donc un dipôle linéaire.

FsΩ1
uti
C
(Farad).
E) Aspect énergétique
1) Effet Joule
R
i
u
2
2
)(
)(
GuGuuiuP
RiiRiiuP
Interprétation microscopique : les porteurs de charge gagnent de l’énergie
cinétique sous la tension et cèdent cette énergie cinétique à cause des chocs avec
le conducteur. Transfert d’énergie = transfert thermique (chaleur).
dtRiQ2
(Effet Joule)
2) Energie magnétique stockée par une bobine
Bobine idéale :
dt
Lid
dt
di
LiiuP )( 2
2
1
. (
dt
di
i
dt
di 2
2
)
On pose
2
2
1LiEm
. Donc
WPdtdE
dt
dE
Pm
m
.
m
E
est donc l’énergie magnétique stockée dans la bobine sous la forme d’un
champ magnétique. Quand
0P
,
m
E
augmente, quand
0P
,
m
E
diminue.
3) Energie électrique stockée par un condensateur
dt
Cud
dt
du
CuiuP )( 2
2
1
.
On pose
2
2
1CuEél
. Donc
WPdtdE
dt
dE
Pél
él
.
él
E
est donc l’énergie électrique stockée par le condensateur sous la forme
d’un champ électrique. Quand
0P
,
él
E
augmente, quand
0P
,
él
E
diminue.
II Générateurs linéaires
A) Sources de tension et de courant idéales
1) Source de tension idéale
C’est un dipôle aux bornes duquel u est constante, quel que soit i.
u
i
e
u
e
i
e : force électromotrice de la source de tension (fém).

2) Source de courant idéale
C’est un dipôle traversé par un courant constant d’intensité constante, quelle
que soit la tension.
j : courant électromoteur ou courant de court-circuit (ccc) de la source.
u
ij
j
i j
ou
B) Source réelle
u
iu
i
g
j
e
j
r
e
Source
réelle
Représentation de Thévenin :
u
e
ir
Caractéristique :
rieu
e : fém de la source
r : résistance interne
Représentation de Norton :
u
j
i
r
guj
r
u
r
e
i
avec
r
e
j
et
r
g1
j : ccc de la source
g : conductance interne.
C) Dipôles linéaires en régime continu
En régime continu, u et i sont indépendants du temps :
0 dt
di
dt
du
Donc l’équation différentielle devient :
ibCua 00
Un dipôle linéaire est donc un générateur linéaire en courant continu.
D) Association en série et en parallèle de dipôles linéaires

1) En série
Dipôles représentés dans le modèle de Thévenin :
u
e1
ir1e2r2enrn
n
kkkk ireu 1
où
1
k
si
k
e
et u sont dans le même sens, -1 sinon.
Donc
n
kk
n
kkk rieu 11 )(
. Une association en série de dipôles linéaires est
donc un dipôle linéaire de fém la somme des fém des dipôles, et de résistance
interne la somme des résistances internes des dipôles.
2) En parallèle
Représentation dans le modèle de Norton :
i
j1
1
1
1g
r
j2
2
1
2g
r
jn
n
g
n
r1
u
Loi des nœuds :
n
kk
n
kkknn gujugjugjugji 11
2211 )(...)(
.
Une association en parallèle de dipôles linéaires est donc un dipôle linéaire
de courant de court-circuit la somme des courants de court-circuit des dipôles, et
de conductance interne la somme des conductances internes des dipôles.
E) Echelon de tension et de courant
e(t) ou j(t)
t
E ou J
1) Echelon de tension
0 si )(
0 si 0)(
tEte
tte
Réalisation :
E
i
2
1
u
Pour
0t
, interrupteur en 2.
0u
Pour
0t
, interrupteur en 1.
Eu
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
 16
16
 17
17
 18
18
1
/
18
100%