Correction

Correction
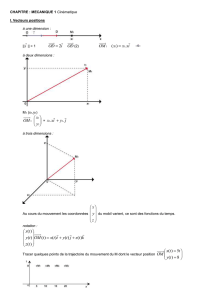
I. Généralités.
1. Il s’agit d’un mouvement plan. Deux coordonnées, donc deux axes, suffisent à décrire la position de la
fourmi.
2. L’échelle est 1/1 ; les mesures de longueur pourront être directement effectuées sur le document...
La durée s’écoulant entre deux positions successives est :  = 1,0 s.
3. Phase 1 : mouvement rectiligne (la trajectoire est une droite) accéléré (la vitesse augmente puisque qu’en
des durées égales, la fourmi parcourt une distance de plus en plus grande (la distance entre les points
augmente)).
Phase 2 : mouvement rectiligne (la trajectoire est une droite) uniforme (la valeur de la vitesse est constante
puisque les points sont équidistants (la fourmi parcourt la même distance en des durées égales)).
Phase 3 : mouvement circulaire (la trajectoire est un arc de cercle) uniforme (les points sont équidistants).
II. Le vecteur position.
1. Voir le document.
2. Composantes : OM29 
3. D’après le théorème de Pythagore : OM29 =  = 
4. On vérifie bien OM29 = 16,6 cm.
5. La norme du vecteur position OM29 est égale à la distance séparant la position finale de la fourmi de
l’origine O du repère.
6. OM 
 : la fourmi se trouve sur l’axe (Oy), 10 cm au dessus de l’origine.
OM 
  : la fourmi se trouve sur l’axe (Ox), 6 cm à gauche de l’origine.
7. Le vecteur position n’est pas constant car la fourmi se déplace...

III. Etude de la phase 1 du mouvement.
1.
Position Mi
ti (s)
Vecteur position OMi
x (cm)
y (cm)
M0
0
0
0
M1
1,0
0,50
0,25
M2
2,0
1,50
0,75
M3
3,0
3,00
1,50
M4
4,0
5,00
2,50
M5
5,0
7,50
3,75
2. Graphes :
x = 0,25t2 + 0,25t
0
2
4
6
8
10
12
0 1 2 3 4 5 6 7
y = 0,125t2 + 0,125t
0
1
2
3
4
5
6
0 1 2 3 4 5 6 7
x (cm)
t (s)
t (s)
y (cm)

3. La modélisation du nuage de points par une courbe polynomiale de degré 2 permet de retrouver les équations
horaires (la courbe est une branche de parabole).
4. OM6 
On retrouve les composantes de ce vecteur position du le document...

Correction
I. Etude de la phase 1 du mouvement.
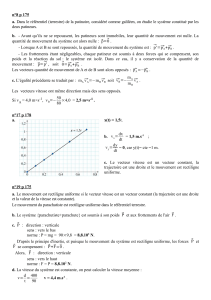
1. Calcul de la vitesse moyenne de la fourmi :
Pour le déplacement d’une fourmi, l’unité la plus adaptée est le cm/s.
La conversion en km/h s’effectue en multipliant la vitesse en m/s par 3,6 (sauriez vous démontrer pourquoi ?)
La vitesse moyenne donne une information limitée : on sait que si la fourmi avait une vitesse constante (ce qui
n’est pas le cas !), elle parcourrait 7,1 km en une heure. Seulement... elle accélère.
2. On applique la relation donnée dans la définition :
Qui devient, pour la vitesse v3 au point M3 :
On remarque que cette relation permet de calculer la vitesse moyenne sur un trajet M2M4.
De même, pour la vitesse v5 au point M5 :
On estime ainsi la valeur d’une vitesse instantanée (à un instant donné).
3. La valeur de la vitesse augmente : il s’agit bien d’un mouvement accéléré.
4. Voir document (échelle 1 cm pour 1cm/s)
5. On mesure les composantes des vecteurs vitesses directement sur la figure :
 et 

6.
Position Mi
ti (s)
Vecteur vitesse vi
vx (cm/s)
vy (cm/s)
vi (cm/s)
M0
0
0,25
0,125
0,28
M1
1,0
0,75
0,375
0,84
M2
2,0
1,25
0,625
1,40
M3
3,0
1,75
0,875
2,0
M4
4,0
2,25
1,125
2,51
M5
5,0
2,75
1,375
3,1
Les valeurs des composantes vx et vy sont directement mesurées sur la figure (échelle 1 cm pour 1 cm/s)
7. Graphes :
Sauriez-vous calculer la vitesse initiale de la fourmi en M0 ?
vx = 0,5t + 0,25
0
0,5
1
1,5
2
2,5
3
3,5
0 1 2 3 4 5 6 7
vy = 0,25t + 0,125
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
0 1 2 3 4 5 6 7
vx (cm/s)
t (s)
t (s)
vy (cm/s)