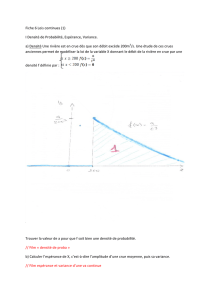
Problème d`informatique : Génération de variables aléatoires

N
M=√N
(xi)1≤i≤M+1
M=√N i
[xi, xi+1[.
`
xi+1 −xi=`
i
i
i
N `

N
χ2
χ2
χ2=1
M
M
X
i=1
b
P[i]−P[i]2
P[i]
Mb P[i]
P[i]i χ2
P[i]
χ2
χ2N
N χ220
U2≤e−1
2(X−1)2
U3≤0,5

σ2
(MIN −MAX)2/12