examen 2012 - ESPCI - Catalogue des Cours

1
EXAMEN D'ELECTRONIQUE
PARTIE A
QCM sans documents ; durée : 45 mn ; barème : 8 points.
PARTIE B
Durée : 2 h 15 ; barème : 12 points.
Documents manuscrits et photocopies de transparents autorisés.
Choix : question III.1 ou question III.2.
REMARQUES PRELIMINAIRES : rappelons quelques péchés mortels pour des
ingénieurs :
• omettre de vérifier l'homogénéité des formules littérales,
• omettre de s'assurer de la vraisemblance des ordres de grandeur (et des
signes) des résultats numériques,
• omettre de faire des approximations évidentes,
• se lancer dans des calculs abracadabrants sans réfléchir (comme les années
précédentes, aucune question de ce problème ne nécessite plus de quatre ou
cinq lignes de calcul une fois que les équations sont correctement posées).
On rappelle que, pour tous les calculs littéraux (et notamment dans la présentation
du résultat final), on doit toujours s'efforcer de faire apparaître des grandeurs sans
dimension.
Il sera tenu le plus grand compte de la précision, de la clarté et de l'élégance de la
rédaction ; les "explications" constituées d'une suite d'équations séparées par des
signes ⇒ sans commentaires ne sont pas acceptables.
Tous les diagrammes de Bode demandés sont les diagrammes asymptotiques.
______________
On considère un transistor NMOS décrit par le modèle le plus simple présenté en
cours (modèle de Shichman-Hodges). Dans tous les circuits considérés ici, le substrat
et la source sont reliés, de sorte que le transistor a toujours le fonctionnement normal
décrit en cours.
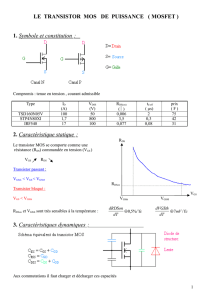
I. Généralités
On rappelle que la transconductance d’un transistor MOS est définie par
g0=∂IDS
∂VGS
⎛
⎝
⎜⎞
⎠
⎟
VDS
.
La Figure 1 représente (aire grisée) le schéma équivalent "petits signaux" d'un
transistor NMOS décrit par le modèle de Shichman et Hodges. Conformément aux
conventions de notation du cours, iDS, vGS, vDS désignent des "petites" variations de ce
courant et de ces tensions, autour d'un point de fonctionnement.

2
Figure 1
I.1. Établir l’expression de g0 pour un transistor NMOS en régime saturé, en
fonction de IDS, VGS, VT.
I.2. On souhaite à présent tenir compte de l’effet Early. On désigne par
I
DS
0
V
GS
( )
le courant drain-source en l’absence d’effet Early :
I
DS
0
V
GS
( )
=
β
2
V
GS
−V
T
( )
2
. En
tenant compte de l’effet Early, l’expression du courant drain-source devient,
en régime permanent :
I
DS
V
GS
,V
DS
( )
=I
DS
0
V
GS
( )
1+ λ V
DS
( )
. Le schéma « petits
signaux » correspondant est représenté sur la Figure 2.
Figure 2
I.2.1. Exprimer la transconductance g en fonction de g0, λ , VDS.
I.2.2. Exprimer la résistance interne r0 en fonction de λ et
I
DS
0
V
GS
( )
; on
pourra, si nécessaire, s’inspirer du calcul analogue effectué pour les
transistors bipolaires.
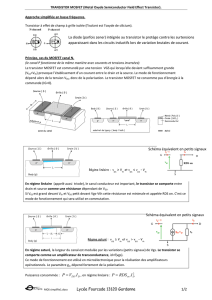
II. Étude sommaire du montage cascode
II.1. On considère le montage représenté sur la Figure 3, où l’on suppose que le
transistor est en régime saturé, et que la résistance de charge RC est infinie.
Conformément aux notations du cours, vGS désigne une petite variation de
tension autour de la tension continue VGS ; la même convention est utilisée
pour la tension de sortie. Dans toute cette partie, on utilisera le modèle de
Shichman et Hodges sans tenir compte de l’effet Early (Figure 1).
II.1.1. Calculer le gain en petits signaux vout/vGS en fonction de g0 et R3.
Application numérique : g0 = 10-3 Ω-1, R3 = 30 k Ω.

3
II.1.2. Tout transistor MOS possède une capacité parasite CGD entre la grille et
le drain.
Figure 3
II.1.2.1. Sans calcul, indiquer la valeur du gain vout/vGS à fréquence
infinie.
II.1.2.2. Sans calcul, indiquer l’expression du gain vout/vGS à très basse
fréquence.
II.1.2.3. Étalir l’expression du gain vout/vGS en fonction de ω , CGD, g0, R3.
II.1.2.4. Préciser ce que signifie, en pratique, l’expression « fréquence
infinie » de la question II.1.2, si CGD = 1 pF, g0 = 10-3 Ω-1, R3 = 30
k Ω.
II.1.2.5. Tracer le diagramme de Bode asymptotique du gain pour les
valeurs numériques de la question précédente.
II.1.2.6. Résumer l’effet de la capacité CGD sur le gain du circuit. Cet
effet est connu sous le nom d’effet Miller.
II.2. On considère à présent le circuit de la Figure 4, appelé montage cascode, où
V+ est une tension de polarisation ; on suppose que les deux transistors sont
saturés, et qu’ils ont la même transconductance g0. On note CGD1 et CGD2 les
capacités grille-drain des transistors T1 et T2. On suppose toujours que la
résistance RC est infinie.

4
Figure 4
II.2.1. Établir le schéma équivalent « petits signaux » de ce circuit en tenant
compte uniquement de la capacité CGD1 (on notera vGS2 la tension grille-
source « petits signaux » du transistor T2).
II.2.2. Exprimer le gain vout/vGS de ce circuit en fonction de ω , CGD1, g0, R3.
II.2.3. Comparer l’évolution du module du gain en fonction de la fréquence
du circuit cascode à celle qui a été établie pour le circuit de la question
II.1. Conclusion ?
II.2.4. Établir les expressions des éléments eTh et RTh du schéma équivalent
selon Thévenin du schéma petits signaux établi à la question II.2.1 en
fonction de ω , CGD1, g0, R3, vGS. Cette question nécessite très peu de calculs.
II.2.5. Modifier le schéma équivalent « petits signaux » établi à la question
II.2.1 pour tenir compte des deux capacité CGD1 et CGD2.
II.2.6. En déduire l’expression du gain complexe du circuit en fonction de ω ,
CGD1, CGD2, g0, R3 (cette question nécessite très peu de calculs). Préciser
l’expression de la pulsation de coupure de ce circuit.
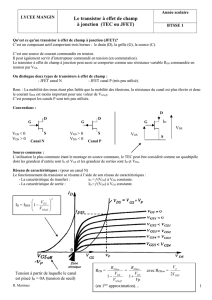
III. Étude d’un étage d’amplification
On considère l’amplificateur dont le schéma est représenté sur la Figure 5. On
suppose dans toute la suite que le transistor est polarisé de telle manière qu’il se
trouve en régime saturé. On suppose toujours que la résistance de charge Rc est
infinie.

5
Choix : question III.1 ou question III.2
III.1. Modèle simple : influence du condensateur C.
III.1.1. Établir le schéma équivalent "petits signaux" de l'amplificateur en
utilisant le modèle de transistor dont le schéma est indiqué sur la
Figure 2.
Figure 5
III.1.2. On désigne par « gain du circuit » le rapport vout / vin en supposant que
la résistance de charge RC est infinie.
III.1.2.1. Exprimer la transconductance g0 du transistor en fonction de
β , VT, VDD, R1, R2.
III.1.2.2. Exprimer le gain Gv∞, à fréquence infinie, du circuit ainsi
modélisé, en fonction de g, RS, R12 = R1 // R2, R'3 = r0 // R3.
III.1.2.3. Exprimer le gain complexe Gv du circuit en fonction de ω , Gv∞,
ω
b, où
ω
b est la pulsation de coupure basse du circuit, que l’on
exprimera en fonction de C, RS, R12.
III.1.3. Tracer le diagramme de Bode asymptotique de Gv avec Gv∞ = −23 et
ω
b = 135 rad/s.
III.2. La grille et le substrat pouvant être considérées comme les armatures d’un
condensateur isolées par l’isolant de grille, tout transistor MOS possède une
capacité grille-substrat CGS. On étudie l’effet de cette capacité seule, en
ignorant l’effet des autres.
III.2.1. Expliquer qualitativement, sans faire de calculs, les effets de CGS sur le
gain à haute fréquence et à basse fréquence.