Matière : Physique Classe : SG. Premier exercice (7pts) : étude

1
Matière : Physique
Classe : SG.
_________________________________________________________
Premier exercice (7pts) : étude énergétique
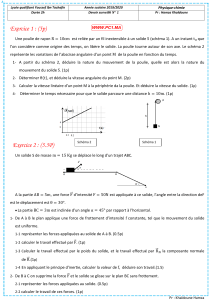
Un jouet d'enfant est formé d'un rail placé dans un plan vertical comme indique la figure ci-dessous. La
partie ABC est un trajet curviligne et la partie CD est un trajet rectiligne incliné sur l'horizontal d'un angle
α =300. Un mobile (M), supposé ponctuelle de masse m=200g peut se déplacer le long de ce rail.
2
.10 smg 
Le niveau de référence de l’énergie potentielle de pesanteur est le plan horizontal passant par B.
A-Mouvement de (M) sur la partie ABC
Le mobile (M) est abandonné sans vitesse initiale de A. il arrive en C avec une vitesse nulle.
a-Calculer l'énergie mécanique du système ((M), Terre) en A, puis celle en C.
b-Comparer les résultats. Que peut-on déduire.
B-Mouvement de (M) sur la partie CD
I-Etude théorique
On néglige le frottement le long de CD. Le mobile (M) part de C à l'instant t =0s sans vitesse initiale et
aborde le plan incliné. A l'instant
t
, (M) passe par la position
J
d'abscisse
xCJ 
avec une vitesse de
mesure
V
a-Calculer CD
b- Montrer que l'énergie potentielle de la pesanteur du système ((M), Terre), a pour expression
instantanée
xEPP  6,1
c- Déterminer en fonction de
x
et
V
l'expression instantanée de l'énergie mécanique du système
((M), Terre)
c-Déduire
D
V
, vecteur vitesse de (M) en D
d-Déterminer
EX
F
, la résultante des forces extérieures appliquées à (M) entre C et D.
e-Déduire la durée nécessaire pour parcourir le trajet CD.
II-Etude graphique
En réalité, un dispositif expérimental assisté par ordinateur, trace les variations de l'énergie cinétique et de
l'énergie potentille de pesanteur du système ((M), Terre) en fonction de
x
lorsque (M) parcourt le trajet
CD. La figure ci- dessous montre ces variations.
B
D
A
C
hC=0,8 m
hA=1 m

2
a- Laquelle des courbes (C1) ou (C2) Montre la variation de l'énergie cinétique de (M). Justifier votre
choix.
b- à partir de deux courbes (C1) et (C2), déduire l'existence d'une force de frottement
f
entre C et D,
puis calculer la variation de l'énergie mécaniques du système ((M), Terre) entre C et D.
Déduire la valeur de
f
c- Déterminer à partir du graphe les expressions de
C
E
et
PP
E
du système ((M), Terre) en fonction de
x
en déduire que l'énergie mécanique du système ((M), Terre) n'est pas conservée entre Cet D
Deuxième exercice : Energie et oscillation
Un pendule élastique horizontal est formé d’un ressort
(R), à spires non jointives, de masse négligeable et de
constante de raideur K, dont l’une de ses extrémités est
fixe et par l’autre extrémité est attaché par un solide (S)
de masse M = 100 g comme le montre la figure (1).
Le solide (S) peut se déplacer le long d’un axe
horizontal
Ox'x
parallèle à l’axe du ressort. Au repos, le
centre d’inertie G de (S) se trouve en O. La position de G est repérée par l’élongation
OGx
.On donne
dt
dx
V
(mesure de la vitesse)
A – Première mode d’oscillation :
On écarte (S) à partir de O de 10 cm dans le sens positif et on le lâche sans vitesse à la date t = 0.
Le solide (S) oscille entre deux positions extrêmes autour de O. On néglige le frottement
1- Quel est, en justifiant, le mode d’oscillation de (S) ?
2-a- Donner l’expression de l’énergie mécanique du système (pendule ; Terre) en fonction de M, K, x et
la mesure de
V
de (S).
b- Déterminer l’équation différentielle qui régit les oscillations de (S).
c- En déduire l’expression de la période T0 des oscillations.
3- Sachant que (S) effectue 5 oscillations en 4,4 s. déduire que K=5,1N/m.
1,6
0,2
0,2 0,4 1,2 1,8
0,4
E (J)
x (m)
O
x'
x
O
(R)
(S)
G
Figure (1)

3
4-a- La solution générale de l’équation différentielle précédente est
t
T
Atx
0
2
cos)(
.
Déterminer
A
et
b-Représenter, pour une période, la variation de
)(tx
en fonction du temps en utilisant l’échelle :
cmcm 51 
en ordonnée et
scm 2,01 
en abscisse
B – Deuxième mode d’oscillation :
On écarte (S) de 10 cm, de sa position d’équilibre et on le lâche. Le graphique de
)(tx
en fonction du
temps est donné dans la figure (2).
1-a- Quel est, en justifiant, le mode d’oscillation de (S) ?
b- Comment varie l’énergie mécanique du système
(pendule ; Terre) ?
Sous quelle forme apparaît sa variation ?
2-a- Trouver, d’après le graphique, la durée
1
t
séparent le
passage de (S) par deux maximums positifs et successifs.
b- Comment appelle-t-on cette durée ?
c- Comparer
1
t
et
0
T
4-a- Calculer l’énergie perdue par l’oscillateur entre les dates
0
0t
et
1
2tt 
b- Déduire la puissance moyenne « p » dissipée par le pendule.
Troisième exercice : Energie mécanique et choc
On considère un pendule simple de longueur L = 90 cm et de masse m = 100 g. Le pendule est dans sa
position d’équilibre, m repose sur un rail horizontal
xx'
. Pour lancer Une particule de masse M = 200 g
sur le rail
xx'
avec une vitesse
v
= v
i
on utilise un ressort de raideur K=100N/m et masse négligeable.
Avant le lancement de M le ressort est comprimé de
0
x
puis lâcher sans vitesse, M entre en choc avec la
masse m du pendule. On néglige le frottement sur le rail
Juste après le choc :
- La particule M se déplace avec la vitesse
ivv 1
1
et monte sur un rail courbé BA, situé dans le plan
vertical de
xx'
d’une hauteur maximale h = 20 cm
-La masse m part avec une vitesse
v
2 = v2
i
et le pendule prend une amplitude maximale
0
60
m
.
Le niveau de référence de l’énergie potentielle de pesanteur est le plan horizontal passant par O.
Prendre g = 10 m/s2.
1- En appliquant la conservation de l’énergie mécanique du système (pendule, Terre),
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
t(s)
-10
-5
0
5
10
x(cm)
Figure (2)
v
X’
X
O
m
M
h
A
i
B

4
vérifier que la vitesse du pendule juste après le choc est
)cos1(2
2mgLv
.
Calculer la valeur de
2
v
2- En appliquant la conservation de l’énergie mécanique du système (M, Terre),
vérifier que la vitesse de M juste après le choc est
ghv2
1
.
Calculer la valeur de
1
v
3- En appliquant la conservation de la quantité de mouvement du système (M, m).
Trouver que la vitesse
v
de M avant le choc a la valeur
1
.5,3  smv
4- Justifier que le choc n’est pas élastique.
5- En appliquant la conservation de l’énergie mécanique du système (M, ressort, Terre) trouver
0
x
6- On suppose que le choc est élastique et que
1
.5,3  smv
.
Trouver alors les nouvelles valeurs de
v
1 et de
v
2.
Quatrième exercice : Vérification de la deuxième loi de Newton
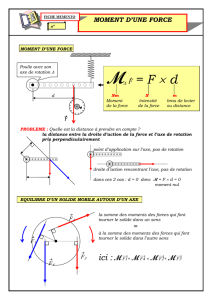
On dispose d'une poulie (D) de masse M = 1 kg et de rayon r = 40 cm et d'un solide (S) de masse,
m = 0,5 kg. Un fil inextensible de masse négligeable est enroulé la gorge de (D), le solide (S) est accroché à
l'extrémité libre du fil (Fig 1). On néglige toute force de frottement et on prend. g = 10 m/s2,
I=Mr2/2 (moment d’inertie de la poulie par rapport à son axe de symétrie
)(
) .
Le niveau de référence de l'énergie potentielle de pesanteur est le plan horizontal (P)
passant par le centre de masse G et perpendiculaire à
)(
A t = 0s, le solide (S) se trouve à une distance
d
de (P), puis il est lâché sans vitesse initiale, la poulie
tourne et le solide se déplace vers le bas. À un instant
t
, le solide aura parcourue une distance
x
et la poulie a tourné d'un angle autour de l’axe de symétrie
)(
1-a-Déterminer l'énergie mécanique du système {Solide, poulie, Terre} à
l'instant t = 0s, en fonction de m, g et
d
b-Déterminer l'expression de l'énergie mécanique du système
{Solide, Poulie, Terre} à l'instant
t
en fonction de m, M, V, g et
x
.
c-En appliquant le principe de conservation de l'énergie mécanique, déduire
l'expression de la vitesse du solide à l'instant
t
en fonction de
x
d- Déduire l'accélération
a
du solide
2- En appliquant la deuxième loi de Newton sur le solide (S), déterminer la
La mesure de la tension T du fil exercée sur le solide(S)
3- En appliquant la deuxième loi de Newton sur la poulie, déterminer la tension
du fil exercée sur la poulie.
4- Calculer la vitesse angulaire
'
et l'abscisse angulaire à l’instant
st 1
1
, en déduire le nombre de tours
effectués durant
st 1
1
.
5- Le fil se rompe à l’instant
st 1
1
. Quelle sera la vitesse angulaire
'
et le nombre de tours effectué durant
?3s
6- á
st 4
2
, on applique un couple de freinage dont le moment est supposé constant pour arrêter le disque
(M = -1 N.m).
a- Déterminer en appliquant le théorème du moment cinétique l’expression de la vitesse angulaire
'
en fonction du temps.
Figure 1
G
(D)
d
Epp = 0

5
b-Déterminer le temps que prend la poulie pour s’arrêter.
c-Quel nombre de tours aura-t-il effectué pendant le freinage ?