TD 22 Travail, puissance et énergie

TD 22 Travail, puissance et énergie
Lycée Polyvalent de Montbéliard - Physique-Chimie - TSI 1 - 2016-2017
Exercice 1 - Application directe du cours :
1. Une rame de train TER possède une masse de 250 tonnes environ. Sa vitesse maximale est de 120 km ·h−1.
Déterminer l’énergie cinétique de ce train à sa vitesse maximale.
2. Un skieur de 80 kg skie sans frotter sur la neige et effectue un dénivelé de 15 m. Sachant qu’il est parti
à l’arrêt, quelle vitesse atteint-il (en km ·h−1) ?
3. Un cycliste, de masse m= 80 kg avec bicyclette incluse, effectue l’ascension du Mont Ventoux. Il roule à
la vitesse constante v= 10.5 km ·h−1sur une pente α= 7% (le pourcentage d’une pente correspond à la
tangente de l’inclinaison du terrain : rapport de la dénivellation sur la distance horizontale parcourue).
(a) Quelle est la puissance Pdu poids ?
(b) Un ordinateur portable consomme environ P0= 50 W. Commenter.
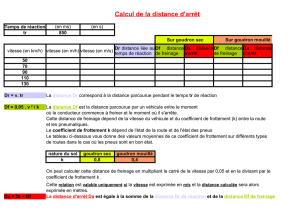
Exercice 2 - Distance de freinage : Une voiture de masse m= 1500 kg roule à la vitesse de 50 km ·h−1
sur une route horizontale. L’automobiliste freine et s’arrête sur une distance de d= 15 m. La force de
freinage est supposée constante.
1. Déterminer le travail de cette force et en déduire sa norme.
2. En supposant que cette force reste inchangée, quelle distance faut-il pour s’arrêter avec une vitesse
initiale de 90 km ·h−1?
Exercice 3 - Mouvement sur plan incliné : On abandonne sans vitesse initiale un cube (considéré
comme un objet ponctuel) de masse msur un plan incliné d’un angle α. Le cube glisse alors sans frottements
sur une longueur Lavant de rencontrer l’extrémité d’un ressort de raideur ket de longueur à vide l0.
1. Déterminer la longueur minimale que peut avoir le res-
sort.
2. Déterminer l’énergie potentielle de la masse avant et
après le contact avec le ressort. En déduire la position
d’équilibre.
L
α
Exercice 4 - Détermination d’un coefficient de frottement : Deux point matériels M (masse m) et
M’ (masse m0) sont reliés par un fil inextensible de masse négligeable susceptible de glisser sur une poulie
fixe (on suppose les frottements nuls au niveau de la poulie). Initialement, le fil est tendu et le point M’
repose sur un support, à une hauteur hdu sol. A t= 0, un opérateur enlève le support et le point matériel
M se met à glisser sur un plan horizontal avec un coefficient de frottement f. On suppose le fil suffisamment
long pour que la masse M s’arrête avant d’atteindre la poulie.
1. Exprimer la distance Dparcourue par M avant
de s’arrêter.
2. En déduire fen fonction de m,m0,het D.
M
M’
h
Exercice 5 - Tunnel terrestre : On démontre que pour tout point M de masse msitué à l’intérieur de
la Terre à la distance rdu centre C de la Terre, l’attraction terrestre est une force agissant sur ce point,
dirigée vers le centre de la terre et de valeur :
Maxime Champion - www.mchampion.fr 1/2

TD 22 : Travail, puissance et énergie Maxime Champion
#”
F=−mg r
RT
#”
eravec #” er=
−−→
CM
|−−→ CM|.
On considère un tunnel rectiligne AB, d’axe (Hx) ne passant pas
par C et traversant la Terre. On note dla distance CH du tunnel
au centre de la Terre. Un point matériel M de masse mglisse sans
frottement dans le tunnel. Ce véhicule part de A sans vitesse initiale.
On prendra RT= 6.4×106m,d=CH = 5 ×106met g= 10 m ·s−2.
•
C
A B
H
•x
1. Déterminer l’énergie potentielle Ep(x)de M.
2. Quelle est la vitesse maximale atteinte par M au cours du mouvement.
3. Déterminer x(t).
4. Représenter le graphe Ep(x)et décrire le mouvement de M à partir de sa position initiale.
5. Déterminer le temps mis pour aller de A vers B.
2/2