LOI DE COMPOSITION DES VITESSES ET DES ACCÉLÉRATIONS

Q Loi de composition des vitesses et des accélérations (33-206) Page 1 sur 4 JN Beury
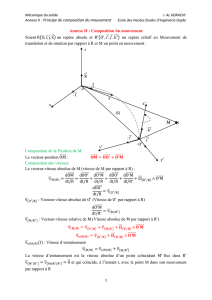
O
O’
M
ℜ
'ℜ
LOI DE COMPOSITION DES VITESSES ET
DES ACCÉLÉRATIONS
I. LOI DE COMPOSITION DES VITESSES
I.1 Deux référentiels – Vitesse absolue – Vitesse relative
On considère deux référentiels :
()
,,,Oi jkℜ=
G
GG
référentiel absolu et
(
)
'',,,OIJKℜ=
G
GG
référentiel relatif.
On est dans le cas le plus général.
• Le point M a pour coordonnées (x, y, z) dans le référentiel
ℜ
d’origine O : OM xi yj zk=++
G
J
JJJGGG
.
La vitesse de M dans le référentiel
ℜ
est appelée vitesse absolue :
()
d
d
a
OM
vM tℜ
=
JJJJG
G.
On peut écrire :
()
d
d
a
OM
vM xi yj zk
tℜ
==++
J
JJJG
G
GG
G
• Le point M a pour coordonnées (X, Y, Z) dans le référentiel '
ℜ
d’origine O’ : 'OM XI YJ ZK=++
J
JJJJG GG G
.
La vitesse de M dans le référentiel '
ℜ
est appelée vitesse relative :
()
'
d'
d
r
OM
vM tℜ
=
JJJJJG
G
On peut écrire :
()
'
d'
d
r
OM
vM XI YJ ZK
tℜ
==++
J
JJJJG
G
GG
G
I.2 Exemple avec le tapis roulant
On considère un point matériel se déplaçant sur un tapis roulant.
Le référentiel absolu est le référentiel terrestre
(
)
,,,Oi jkℜ=
G
G
G
.
Le référentiel relatif est le référentiel lié au tapis :
(
)
'',,,Oi jkℜ=
G
G
G
avec , et
I
iJ j K k
=
==
G
G
GG
G
G
.
Dans cet exemple, 'ℜ est en translation rectiligne uniforme par rapport à
ℜ
avec
(
)
0
'vO vi
ℜ=G
G
.
La vitesse absolue du point M est la vitesse de M par rapport au sol.
La vitesse relative du point M est la vitesse de M par rapport au tapis roulant.
I.3 Changement de référentiel
On revient dans le cas général avec
()
,,,Oi jkℜ=
G
GG
et
(
)
'',,,OIJKℜ=
G
GG
.
''OM OO O M=+
JJJJG JJJJG JJJJJG
dd'd'
ddd
OM OO O M
ttt
ℜℜ ℜ
=+
JJJJG JJJJG JJJJJG
. Le premier terme est la vitesse de O’ dans
ℜ
. On utilise la formule fondamentale
de la dérivation vectorielle pour le deuxième terme : '/
'
dd ^
dd
AA
A
tt
ω
ℜℜ
ℜℜ
=+
G
G
G
G avec '
A
OM=JJJJJG
G
.
On obtient :
()
'/
'
dd'
'^'
dd
OM O M
vO OM
tt
ω
ℜℜ
ℜ
ℜℜ
=+ +
JJJJG JJJJJG
J
JJJJG
G
G. D’où :
() () ()
{
}
'/
''^'vM vM vO OM
ω
ℜℜ
ℜℜ ℜ
=+ +
J
JJJJG
G
GG G

Q Loi de composition des vitesses et des accélérations (33-206) Page 2 sur 4 JN Beury
O
O’
M
ℜ
'ℜ
I.4 Interprétation avec le point coïncidant – Vitesse d’entraînement
Soit P un point fixe dans 'ℜ :
() ()
'
vP vP
ℜℜ
=
GG
()
{
}
'/
'^'vO OP ω
ℜℜ
ℜ
++
J
JJJG
G
G
.
Dans la suite, on ne va pas prendre un point P quelconque dans '
ℜ
:
On définit P le point coïncidant avec M à l’instant t : c’est un point M fixe dans '
ℜ
et qui coïncide avec M à l’instant
t (on a OM OP=
JJJJGJJJG
à l’instant t).
On peut donner l’image suivante : le point coïncidant avec M à l’instant t est un point collé (Super Glue) à '
ℜ
qui
l’emporte lors de sons mouvement. Si M et P coïncident à un instant t, ils n’ont plus de raison de coïncider après t.
La vitesse de ce point coïncidant dans ℜ est donc :
() ()
'
vP vP
ℜℜ
=
G
G
()
{
}
'/
'^'vO OP ω
ℜℜ
ℜ
++
JJJJG
G
G
.
Comme OM OP=
JJJJGJJJG
, alors
() ()
'
vP vP
ℜℜ
=
GG
()
{
}
'/
'^'vO OM ω
ℜℜ
ℜ
++
J
JJJJG
G
G
On définit la vitesse d’entraînement de M à l’instant t :
La vitesse d’entraînement de M à l’instant t = vitesse absolue du point coïncidant avec M à l’instant t
() () ()
'/
'^'
e
vM vP vO OM ω
ℜℜ
ℜℜ
== +
JJJJJG
G
GGG
On a donc interprété le {} rencontré dans le paragraphe précédent.
I.5 Loi de composition des vitesses
vitesse absolue de M = vitesse relative de M + vitesse d’entraînement de M
(
)
(
)
(
)
are
vM vM vM=+
G
GG
On a deux méthodes pour calculer la vitesse d’entraînement de M
• Première méthode :
(
)()
'/
'^'
e
vM vO OM ω
ℜℜ
ℜ
=+
J
JJJJG
G
G
G
• Deuxième méthode : définir et chercher la trajectoire du point coïncidant avec M à l’instant t. La vitesse
d’entraînement de M est alors la vitesse absolue du point coïncidant avec M à l’instant t.
I.6 Retour à l’exemple du tapis roulant
Pour illustrer sur un exemple concret, on suppose que la vitesse relative vaut 3 m.s-1 et la vitesse d’entraînement vaut 4
m.s-1. On a vu que les deux référentiels sont en translation rectiligne uniforme.
• vitesse relative = vitesse de M par rapport au tapis roulant : 3 m.s-1
• Comment calculer la vitesse d’entraînement ? On a deux méthodes :
Méthode 1 : appliquer la formule démontrée dans le cours :
(
)
(
)
'/
'^'
e
vM vO OM ω
ℜℜ
ℜ
=+
JJJJJG
G
G
G. Ici '/ 0
ω
ℜℜ
=
G
G car '
ℜ
est en translation par rapport à ℜ. On a alors
(
)
(
)
'4
e
vM vO i
ℜ
==
G
G
G.
On a une vitesse d’entraînement de 4 m.s-1.
Méthode 2 : raisonner sur le point coïncidant. On considère donc un point coïncidant avec M à l’instant t, c'est-à-
dire un point collé au tapis roulant et qui se trouve au même endroit que M à l’instant t. Ce point collé a un
mouvement rectiligne uniforme de vitesse 4 m.s-1. La vitesse d’entraînement est par définition la vitesse absolue du
point coïncidant, c'est-à-dire 4 m.s-1, d’où
(
)
4
e
vM i=
G
G
.
II. LOI DE COMPOSITION DES ACCÉLÉRATIONS
II.1 Changement de référentiel
On considère deux référentiels :
()
,,,Oi jkℜ=
G
GG
référentiel absolu et
(
)
'',,,OIJKℜ=
G
GG
référentiel relatif.
On est dans le cas le plus général.
On a vu que : ''OM OO O M=+
JJJJG JJJJG JJJJJG
On a démontré dans le paragraphe précédent :
()
'/
'
dd'
'^'
dd
OM O M
vO OM
tt
ω
ℜℜ
ℜ
ℜℜ
=+ +
J
JJJG JJJJJG JJJJJG
G
G
On dérive une nouvelle fois par rapport au temps dans le référentiel
ℜ
.

Q Loi de composition des vitesses et des accélérations (33-206) Page 3 sur 4 JN Beury
()
2
'/
2
'
d'
ddd'
^'
dddd
vO
OM O M OM
tttt
ω
ℜ
ℜℜ
ℜℜ
ℜ
ℜ
=+ +
JJJJG JJJJJG
G
J
JJJJG
G
()
(
)
2
''/
'/
2
dd
dd'
'^'^
dddd
vM
OM O M
aO OM
tttt
ωω
ℜℜℜ
ℜℜ
ℜ
ℜ ℜ
ℜ
=+ + +
JJJJG JJJJJG
GG
J
JJJJG G
G
On applique deux fois la formule fondamentale de la dérivation vectorielle :
() () () ()
''/
'/ '/ '/
'
'
'
ddd'
'^^'^^'
ddd
vM OM
a M aO v M OM OM
ttt
ω
ωωω
ℜℜℜ
ℜℜ ℜℜ ℜℜ
ℜℜ ℜ
ℜ
ℜ
=+ + + + +
J
JJJJG
G
G
J
JJJJG JJJJJG
GGG
GG G
() () () ()
()
'/
'/ '/ '/
''
d
2^ ' ^' ^ ^'
d
a M a M v M a O OM OM
t
ω
ωωω
ℜℜ
ℜℜ ℜℜ ℜℜ
ℜℜ ℜ ℜ
=+ + + +
G
J
JJJJG JJJJJG
GGG
GG G G
II.2 Interprétation avec le point coïncidant – Accélération d’entraînement
Soit P un point fixe dans 'ℜ :
() ()
'
aP aP
ℜℜ
=
GG
()
'/ '
2^vP ω
ℜℜ ℜ
+
G
G
()
()
'/
'/ '/
d
'^'^^'
d
aO OP OP
t
ωωω
ℜℜ
ℜℜ ℜℜ
ℜ
++ +
G
J
JJJG JJJJG
GG
G.
Dans la suite, on ne va pas prendre un point P quelconque dans '
ℜ
:
On définit P le point coïncidant avec M à l’instant t : c’est un point M fixe dans '
ℜ
et qui coïncide avec M à l’instant
t (on a OM OP=
JJJJGJJJG
à l’instant t).
On peut donner l’image suivante : le point coïncidant avec M à l’instant t est un point collé (Super Glue) à '
ℜ
qui
l’emporte lors de sons mouvement. Si M et P coïncident à un instant t, ils n’ont plus de raison de coïncider après t.
L’accélération de ce point coïncidant dans ℜ est donc :
() ( )
()
'/
'/ '/
d
'^'^^'
d
a P aO OP OP
t
ωωω
ℜℜ
ℜℜ ℜℜ
ℜℜ
=+ +
G
J
JJJG JJJJG
GG
G
G.
Comme OM OP=
JJJJGJJJG
, alors
() ( )
()
'/
'/ '/
d
'^'^^'
d
aP aO OM OM
t
ωωω
ℜℜ
ℜℜ ℜℜ
ℜℜ
=+ +
G
J
JJJJG JJJJJG
G
G
GG
On définit la vitesse d’entraînement de M à l’instant t :
L’accélération d’entraînement de M à l’instant t = accélération absolue du point coïncidant avec M à l’instant t
() () ()
()
'/
'/ '/
d
'^'^^'
d
e
aM aP aO OM OM
t
ωωω
ℜℜ
ℜℜ ℜℜ
ℜℜ
== + +
GJJJJJG JJJJJG
G
G
GG G
II.3 Loi de composition des accélérations
On a vu dans le paragraphe II.1 que :
() ()
{}
()
()
()
{}
'/
'/ '/ '/
'
d
'^'^^'2^
dr
a M a M aO OM OM v M
t
ωωω ω
ℜℜ
ℜℜ ℜℜ ℜℜ
ℜℜ ℜ
=++ + +
GJJJJJG JJJJJG
G
GG
GG G G
• Le premier terme est l’accélération relative de M
• Le deuxième terme est l’accélération d’entraînement de M
• Il reste un troisième terme ! Ce terme est appelé accélération complémentaire ou accélération de Coriolis.
Loi de composition des accélérations : accélération absolue de M = accélération relative de M + accélération
d’entraînement de M + accélération de Coriolis de M.
()
(
)
(
)
(
)
arec
aM aM aM aM=++
GGGG
L’accélération de Coriolis vaut :
()
(
)
'/
2^
cr
aM vM ω
ℜℜ
=
G
GG
On a deux méthodes pour calculer l’accélération d’entraînement de M :
• Première méthode :
() ()
()
'/
'/ '/
d
'^'^^'
d
e
aM aO OM OM
t
ωωω
ℜℜ
ℜℜ ℜℜ
ℜ
=+ +
G
J
JJJJG JJJJJG
G
G
G
G
• Deuxième méthode utilisée le plus souvent dans les exercices : définir et chercher la trajectoire du point
coïncidant avec M à l’instant t. L’accélération d’entraînement de M est alors l’accélération absolue du point
coïncidant avec M à l’instant t.

Q Loi de composition des vitesses et des accélérations (33-206) Page 4 sur 4 JN Beury
z
O
ω
t
M
H
i
G
j
G
k
G
I
G
J
G
z
O
ω
t
M
H
II.4 Deux cas particuliers TRÈS IMPORTANTS rencontrés dans les exercices
a) Référentiel en translation
Soit
()
'',,,Oi jkℜ= G
GG
un référentiel en translation par rapport à
(
)
,,,Oi jkℜ=
G
G
G
.
On a vu que '/ 0
ω
ℜℜ =G
G.
http://www.sciences.univ-nantes.fr/physique/perso/gtulloue/Meca/Cinematique/entrainement_trans.html
Si 'ℜ est en translation par rapport à ℜ :
(
)
(
)
'
e
vM vO
ℜ
=
G
G et
(
)
(
)
'
e
aM aO
ℜ
=
G
G
b) Référentiel en rotation uniforme autour d’un axe fixe
On considère
()
',,,OI Jkℜ= G
G
G
un référentiel en rotation uniforme par rapport à
()
,,,Oi jkℜ= G
GG
autour de l’axe
()
,Ok
G
.
http://www.sciences.univ-nantes.fr/physique/perso/gtulloue/Meca/Cinematique/entrainement_rot.html
Exemple :
()
,,,Oi jkℜ=
G
GG
référentiel géocentrique et
()
',,,OI Jkℜ= G
GG
référentiel terrestre.
On note '/ k
ω
ω
ℜℜ =G
Gavec cte
ω
= .
Il y a une seule façon de calculer l’accélération de Coriolis :
(
)
(
)
'/
2^
cr
aM vM ω
ℜℜ
=
G
G
G
Deux méthodes pour calculer l’accélération d’entraînement :
• Première méthode : Application de la « grosse formule » :
() ()
'
e
aM aO
ℜ
=
GG '/
d
dt
ω
ℜℜ
+
G
()()
'/ '/ '/ '/
^' ^ ^' ^ ^'OM OM OM ωω ωω
ℜℜ ℜℜ ℜℜ ℜℜ
+=
JJJJJG JJJJJG JJJJJG
G
GGG
avec O’ = O.
On fait intervenir le point H projeté orthogonal de M sur l’axe Oz :
()
'/ '/
^^
e
aM OH ωω
ℜℜ ℜℜ
=JJJJG
GG
G
(
)
(
)
'/ '/
^^
H
M ωω
ℜℜ ℜℜ
+
J
JJJG
GG . La formule du double produit vectoriel donne :
()
(
)
'/ '/ '/
^^
e
a M HM HM ωω ω
ℜℜ ℜℜ ℜℜ
==⋅
JJJJG JJJJG
GG G
G
()
() ()
22
'/
H
MHM ωω ω
ℜℜ−=−
J
JJJG JJJJG
G
• Deuxième méthode : Elle est préférable dans les problèmes de concours et permet une interprétation
physique.
Le point coïncidant décrit un cercle de centre H, de rayon HM avec H le projeté orthogonal de M sur l’axe
Oz.
Dans l’exemple, le point coïncidant est un point collé au référentiel terrestre.
()
',,,OI Jkℜ= G
GG est un référentiel en rotation uniforme autour d’un axe fixe par rapport à
()
,,,Oi jkℜ= G
GG . Le mouvement du point coïncidant est circulaire uniforme donc
()
2
e
aM HM ω =−
J
JJJG
G.
Interprétation physique : pour un mouvement circulaire, l’accélération est centripète dirigée vers le centre
de rotation.