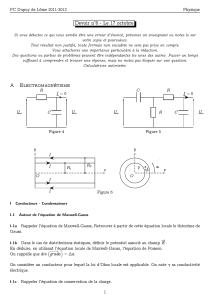
Equations de Maxwell

z= 0 σ−→
E = E(z)−→ uz
E(z)−→
E−→
E
−→
E = E0−→ urE0
ρ(r) div (f−→ ur) =
1
r2
∂(r2f)
∂r
r= R
−→
E
R1R2h
h
V1V2
V(r)
∆V = 1
r
∂
∂r r∂V ∂r 
E(r)
σ
R1
R2
z
vide
h
q q n0
q
r
n+(r) = n0e−
qV
kBTn−(r) = n0e
qV
kBT

ρ(r)
V(r)
V(r) ∆V = 1
r
d2(rV(r))
dr2
qV≪kBT
r→0 V = q
4πε0r
m q =− |e|
x∈[0; L] v(x)
n(x) V(x) V(x= 0) = 0
UI
x
x= 0 x= L
(C) (A)
v(x) V(x)e m
v(0) = 0
x)x
n(x)v(x)eI(x) = I I >0
V(x)
d2V
dx2=I ε0Sm 2e
1
V(x)
V(x) = αx
Lβα β
I U3/2
z=−d
2z=d 2
−→
j=j−→ ex
•−→ B (x, y, z) = B(z)−→ ey
•−→ B|z|> d/2|z|< d/2
B(z)
•−→ rot −→ B = µ0
−→
j