Les statistiques descriptives: mesures de tendance centrale et de

1
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
1
Les statistiques descriptives: mesures de
tendance centrale et de dispersion (1ière partie)
&
Les statistiques descriptives en R (2ième partie)
2 Ressources supplémentaires
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
Compléments de mathématiques.
• http://math.cmaisonneuve.qc.ca/alevesque/m101.html
Il est de votre responsabilité de vous
assurer que vous comprenez les
concepts de base en mathématiques!
3
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
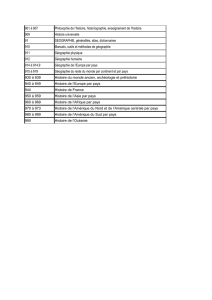
Lettres greques couramment utilsées en statistique
Notes des cours Borcard (2006)

2
4 Statistiques descriptives
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
• Données sont essentielles pour la science! Mais devons-nous
communiquer toutes les données que nous recueillons?
• Paramètres de position: valeurs centrales autour desquelles se
groupent les valeurs observées ! moyenne arithmétique,
moyenne géométrique, moyenne harmonique, médiane, mode
• Paramètres de dispersion: ils renseignent quant à l’étalement de
la distribution des valeurs autour des valeurs centrales ! variance,
écart type, erreur standard de la moyenne
Ex: des tableux des représentations graphiques
Après notes des cours Proulx (2006) et Borcard (2006).
5 Moyenne arithmétique
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
Après notes des cours Borcard (2006).
• avec Yi = valeur de chaque observation individuelle
• avec n = nombre d'observations Yi tirée de l'ensemble de la
population avec N éléments:
• Important: il y a une différence entre les statistiques (échantillon:
d’un échantillon) et les paramètres (population: de la population)
Y
_
=
Yi
i=1
n
∑
n
≠ µ =E(Y)=Yipi
i=1
n
∑
Espérance d'une variable
aléatoire discrète (séance 4)
y
_
=
Yi
i=1
n
∑
N
Y
_
y
_
6 Loi des grandes nombres
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
Après notes des cours Borcard (2006).
• Lorsque n d’un échantillon devient grand,
! les fréquences relatives estimées tendent vers les probabilités et
! les distributions de fréquence relatives observées tendent vers
les distributions de probabilités
• On dit: « is an unbiased estimator of µ »: Yi sont aléatoires et
indépendants, et la population est décrit par une variable aléatoire
normale.
lim
n→∞
Yi
i=1
n
∑
n=Yn
_
$
%
&
&
&
&
'
(
)
)
)
)
=E(Y)= µ
Espérance d'une variable
aléatoire normal (séance 4)
Y
_
n

3
7
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
Moyenne géométrique
• Variable aléatoire log-normale: Y
• Variable aléatoire Z = ln(Y) ! variable aléatoire normale
! Y = eZ
avec e = base du logarithme naturel (~2,71828 ….)
GY: « back-transformed » moyenne
GY=e
1
nln(Yi)
i=1
n
∑
"
#
$
$
%
&
'
'
• Variable aléatoire non-normale: Y
• Variable aléatoire Z = 1/Y ! variable aléatoire normale
! HY: « subcontrary » moyenne
• > GY > HY mais pour Y1 = Y2 = Y3 ….. Yi ! = GY = HY
8 Moyenne harmonique
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
€
HY=1
n
1
Yi
i=1
n
∑
Y
_
n
Y
_
n
9 Médiane
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
• MeY: la valeur de la variable qui se suite au centre de la série
statistique, classée en ordre croissant
• MeY sépare la série en deux groupes d’égale importance
• S’il y un nombre impair d’observation, MeY est une observation de la
série. Exemple: pour la série [1, 32, 128, 129, 1000235], MeY = ?
• S’il y a un nombre pair d’observations, MeY est située entre les deux
observations centrale de la série. Par convention, on utilise la
moyenne de ces deux valeurs. Exemple: pour la série [1, 32, 128,
129, 532, 1000235], MeY = ?
Notes des cours Borcard (2006).

4
10 Mode
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
Notes des cours Borcard (2006).
• MoY: la valeur d’une variable ayant la plus forte fréquence.
• Pour une variable discrète comportant peu de classes, on trouve la
classe la plus fréquence. Sa valeur est le mode. Pour une variable
continue on divise celle-ci en classes
• Une distribution de fréquences a plusieurs modes si on veut mettre
en évidence le fait qu’elle a plusieurs classes non contiguës dont la
fréquence est nettement plus élevée que celle des autres classes.
11 Comparaison entre moyenne a., médiane, mode
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
Y
_
) )
Y
_
Y
_
Y
_
Après notes des cours Proulx (2006) et Borcard (2006).
12 En utilisant différentes paramètres de position
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
• : commodité; Théorème Central Limite: de de grands échantillons
sont conformes à la distribution normale ! il est facile de tester des
hypothèses sur la base de cette propriété (séance 6)
• GY: processus multiplicatifs ! e.g., taux de croissance démographique
• HY: bonne question .... Je ne sais pas beaucoup sur moi-même!
• MeY:
• MoY:
Y
_
Important: ne pas faire confiance à aucun de
ces paramètres de position sans paramètres
de dispersion!
Y
_
} particulièrement utile lorsque les distributions des
observations ne suivent pas une distribution de probabilité
standard

5
13 Variance et écart type d’une population
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
• Avec la loi de grande nombres, la variance d’une population:
• et l’écart type d’une population:
• et la somme des carrés:
• SSY est d'une importance fondamentale pour l'analyse de
régression (séance 9) et l'analyse de la variance (séance 10)
s2=1
n(Yi−Y
_
)2
∑
= σ
2(Y)=E Y −E(Y)
[ ]
2
Variance d'une
variable aléatoire
discrète (séance 4)
SSY=(Yi−Y
_
)2
∑
s=s2
14 Degré de liberté
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
• Degré de liberté: nombre de « pièces d'information indépendantes »
que nous avons dans un ensemble de données pour l'estimation des
statistiques.
• Exemple: échantillon avec n = 1 ! s2 = σ2 = 0
! Toutes les « pièces d'information indépendantes » sont
utilisées pour calculer la moyenne arithmétique, donc il n'y a
pas de « pièces d'information indépendantes » pour calculer s2
and/or σ2!
15 Variance et écart type d’une échantillon
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
• « Unbiased estimator » s2 pour σ2:
• « unbiased estimator » s pour σ:
s2=1
n−1(Yi−Y
_
)2
∑
s=1
n−1(Yi−Y
_
)2
∑
Important: n – 1 règle pour les degrés de
liberté: au moins deux observations sont
nécessaires pour calculer s2 et/ou s!