Document

Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
1
Les statistiques descriptives: mesures de
tendance centrale et de dispersion (1ière partie)
&
Les statistiques descriptives en R (2ième partie)

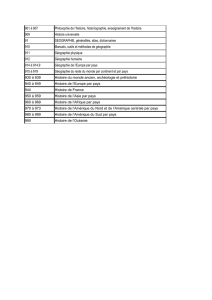
2 Ressources supplémentaires
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
Compléments de mathématiques.
• http://math.cmaisonneuve.qc.ca/alevesque/m101.html
Il est de votre responsabilité de vous
assurer que vous comprenez les
concepts de base en mathématiques!

3
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
Lettres greques couramment utilsées en statistique
Notes des cours Borcard (2006)

4 Statistiques descriptives
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
• Données sont essentielles pour la science! Mais devons-nous
communiquer toutes les données que nous recueillons?
• Paramètres de position: valeurs centrales autour desquelles se
groupent les valeurs observées ! moyenne arithmétique,
moyenne géométrique, moyenne harmonique, médiane, mode
• Paramètres de dispersion: ils renseignent quant à l’étalement de
la distribution des valeurs autour des valeurs centrales ! variance,
écart type, erreur standard de la moyenne
Ex: des tableux des représentations graphiques
Après notes des cours Proulx (2006) et Borcard (2006).

5 Moyenne arithmétique
Oliver Sonnentag, PhD: GÉO1512 – Géographie Quantitative I Séance 5: 29 octobre 2012
Après notes des cours Borcard (2006).
• avec Yi = valeur de chaque observation individuelle
• avec n = nombre d'observations Yi tirée de l'ensemble de la
population avec N éléments:
• Important: il y a une différence entre les statistiques (échantillon:
d’un échantillon) et les paramètres (population: de la population)
Y
_
=
Yi
i=1
n
∑
n
≠ µ =E(Y)=Yipi
i=1
n
∑
Espérance d'une variable
aléatoire discrète (séance 4)
y
_
=
Yi
i=1
n
∑
N
Y
_
y
_