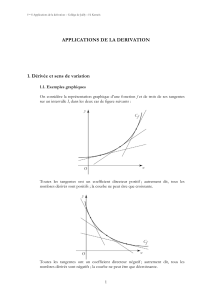
Dérivation sur un intervalle - Classe B/L

Cn
E F E F
FE={f:E→F}
RRR R
R[0,+∞[[0,+∞[R
(R+∗)R
RN
n f n f
f(0) =f, f(1) =f0,∀n>1, f(n)=f(n−1) 0= (f0)(n−1)
f n I (n−1) I f(n−1)
I

• C0(I)I
• C1(I)I
I f0I
• Cn(I)n I
n I n f(n)I
• C∞(I)I
C∞(I)⊂ · · · ⊂ Cn+1(I)⊂ Cn(I)⊂ · · · ⊂ C1(I)⊂ C0(I)⊂RI
n
a∈R
f0:x7−→ xn, fa:x7−→ (x−a)n
f0faC∞R
∀k∈N,∀x∈R, f(k)
0(x) = n(n−1)(n−2) · · · (n−k+ 1)xn−kk6n
0k > n
∀k∈N,∀x∈R, f(k)
a(x) = n(n−1)(n−2) · · · (n−k+ 1)(x−a)n−kk6n
0k > n
C∞RPdeg(P) = n
deg P(k)=n−k k 6n
−∞ k > n
a∈R
f0:x7−→ 1
x, fa:x7−→ 1 x−a
f0faC∞
∀k∈N,∀x∈R∗, f(n)
0(x) = (−1)nn!
xn+1
∀k∈N,∀x∈R\ {a}, f(n)
a(x) = (−1)nn!
(x−a)n+1

n= 0 fa0I∀x∈I, fa(x) = (−1)00!
(x−a)0+1
n>0n
f(n):x7→ (−1)nn!
(x−a)n+1 I x 7→ (x−a)n+1
f(n+ 1) I
∀x∈I, f (n+1)(x) = (−1)nn!×−(n+ 1)
(x−a)n+2 =(−1)n+1(n+ 1)! (x−a)n+2
ga:x7−→ 1
a−xC∞]a, +∞[ ] − ∞, a[x∈R\ {a}
∀n∈N, g(n)
a(x) = n!
(a−x)n+1
C∞R
∀n∈N,∀x∈R,exp(n)(x) = exp(x)
ln C∞]0,+∞[
∀n∈N,∀x > 0,ln(n)(x) = (−1)n−1(n−1)!
xn
C∞
n∈Nx∈R
sin(n)(x) = sin x+nπ
2cos(n)(x) = cos x+nπ 2

Cn
Cn(I, R)RI
f g CnI λ ∈R
(λf +g)Cn
(αf +g)(n)=αf (n)+g(n)
f g CnI(fg)
Cn
(fg)(n)=
n
k=0
n
kf(k)g(n−k)=
n
k=0
n
kf(n−k)g(k)
I J f :I→Rg:J→Rf(I)⊂J
fCnI g CnJ g ◦fCn
α∈Rfα=x7→ xα=eαln(x)C∞]0,+∞[
∀n∈N,∀x > 0, α(α−1) · · · (α−n+ 1)xα−n
a > 0fa:x7→ ax=exln(a)C∞R
∀n∈N,∀x∈R, f(n)
a(x) = (ln(a))nax
f g CnI g
I x 7→ f(x)
g(x)CnI
f[a, b]Cn[a, b[
f(n)` b f Cn[a, b]f(n)(b) = `
I a ∈I
f I a C1I\ {a}
f0a f C1I
f0(a) = lim
x→af0(x)
a

f I x0∈I
fx0α > 0
∀x∈[x0−α, x0+α]∩I, f(x)6f(x0)
fx0α > 0
∀x∈[x0−α, x0+α]∩I, f(x)>f(x0)
f I x0I
f x0f0(x0) = 0
f0(x0) = 0 f x0
x0I f0(x0)=0
a b a < b
f[a, b]→R
f[a, b]
f]a, b[
f(a) = f(b)
c∈]a, b[f0(c) = 0
f[a, b]f
M= sup
[a,b]
f=f(c)m= inf
[a,b]f=f(d)
m=M∀x∈[a, b]m6f(x)6M=m f(x) = m f [a, b]
∀c∈]a, b[, f0(c) = 0
m<M m<f(a)f(a)< M m >f(a)f(a)>M
M6f(a)6m<M
m<f(a) = f(b)f(d)< f(a) = f(b)
d[a, b]f d f d f0(d)=0