chapitre 1 - WebCampus

UNIVERSITE DE NAMUR
Faculté de Médecine
BIOSTATISTIQUE
CLINIQUE
Jacques JAMART
Syllabus partiel du cours « Biostatistique »
1er Baccalauréat en Médecine
Syllabus partiel du cours « Introduction aux Statistiques Médicales »
2ème Baccalauréat en Sciences Biomédicales
2ème Baccalauréat en Sciences Pharmaceutiques
8ème édition
2015

2
Avant-Propos
Ces notes de Biostatistique Clinique représentent la seconde partie du cours
d’« Introduction aux Statistique Médicales » des deuxièmes Baccalauréats en Sciences
Biomédicales et en Sciences Pharmaceutiques, et celle du cours de « Biostatistique » du
premier Baccalauréat en Médecine de l'Université de Namur, anciennement Facultés
Universitaires Notre Dame de la Paix. Elles supposent connues des notions fondamentales de
statistique descriptive et inférentielle telles que les variables aléatoires, les distributions
d’échantillonnage, le principe de l’estimation statistique et des tests, ainsi que les techniques
d’inférence de base comme les comparaisons de fréquences et de moyennes, la corrélation et
la régression, ces notions étant couvertes par la première partie du cours donnée par le
Professeur Eric Depiereux dont ces notes se veulent le prolongement. L’objet de cet
enseignement de Biostatistique Clinique est en effet de montrer l’application des concepts et
des méthodes statistiques aux problèmes spécifiquement médicaux tels que l’épidémiologie et
la recherche des causes des maladies, l’évaluation d’un test diagnostique, l’analyse des
données de survie, les essais cliniques de médicaments ou d’autres thérapeutiques, la méta-
analyse d’un ensemble d’études scientifiques et les applications de biochimie clinique. Son
objectif est de permettre aux futurs médecins, pharmaciens ou chercheurs dans le domaine
biomédical une lecture plus critique de la littérature et une discussion plus nuancée des
informations scientifiques dont ils auront connaissance.

CHAPITRE 1
STATISTIQUE
EPIDEMIOLOGIQUE
1. Types de mesures en épidémiologie
2. Mesures de mortalité
3. Mesures de morbidité
4. Mesures d’association et classification des études
5. Etudes de cohorte
6. Enquêtes cas-témoins
7. Biais
8. Facteurs de confusion
9. Comparaison des études de cohorte et des enquêtes cas-
témoins
10. Jugement de causalité

4
1. Types de mesures en épidémiologie
L'épidémiologie utilise plusieurs types de mesures, qui sont souvent confondues, les
proportions, les ratios, les cotes ou odds et les taux.
Une proportion est un rapport entre le nombre d'éléments d'un groupe et le nombre
d'éléments d'une population plus large contenant ce groupe. C'est une fraction dans laquelle le
numérateur est inclus dans le dénominateur. Elle est souvent multipliée par le facteur d'échelle 100
pour obtenir un pourcentage. Par exemple, dans une population comprenant 60 femmes (f) et 40
hommes (m), la proportion de femmes est évidemment
6,0
406060 m f f
p
Un ratio est un rapport des fréquences de deux classes mutuellement exclusives d'une
même variable. Le ratio femmes/hommes est dans l'exemple
5,1
40
60
m
f
r
Si la variable étudiée n'a que deux classes, le ratio est équivalent à la cote ou odd, rapport entre une
proportion et son complémentaire
ψ=
p - 1p
=
60,- 1 6,0
= 1,5
Un taux est, de façon générale, le changement instantané d'une quantité rapporté au
changement unitaire d'une autre quantité. En épidémiologie, c'est le rapport entre un nombre de
sujets présentant un évènement et la population à risque pour cet évènement pendant une période
donnée. L'unité du numérateur est donc un nombre de sujets et celle du dénominateur un nombre
de sujets multiplié par une unité de temps, habituellement des personnes-années. Si, dans une
population de taille N suivie pendant un temps T, n sujets présentent un évènement qui survient
après un délai variable, soit tj pour le sujet j, le nombre de personnes-temps à risque est, de façon
exacte,
PT =
n
1j
jT n) - (N t
Si on ne connait pas les délais d'apparition individuels de l'évènement tj et si l'on suppose qu'ils
suivent une distribution uniforme pendant la période considérée, on peut remplacer leur somme par
le nombre de sujets multiplié par le délai moyen d'apparition et calculer PT de façon approchée par
PT ≈
2
Tn
(N - n) T = (N -
2
n
) T
En épidémiologie, on étudie 3 types de paramètres, des mesures de mortalité et de morbidité qui
concernent l’épidémiologie descriptive, et des mesures d’association qui font partie de
l’épidémiologie analytique.

5
2. Mesures de mortalité
Selon la définition d'un taux donnée plus haut, un taux de mortalité est le rapport entre un
nombre de décès et le nombre de personnes-temps à risque pour cet évènement. On parle de taux
de mortalité brut lorsque ce paramètre est estimé sur l'ensemble d'une population et de taux de
mortalité spécifique lorsque l'on ne considère que les sujets appartenant à une certaine catégorie
de la population, appelée strate, ou que les décès dus à une maladie particulière. On ne peut
évidemment étudier valablement des taux de mortalité‚ que si les populations dont ils proviennent
sont comparables, c'est-à-dire si les proportions de sujets des différentes strates des populations
sont identiques (sexe, âge, ...). Les taux de mortalité‚ doivent donc être ajustés ou "standardisés" en
fonction d'une population de référence. Il y a deux types d'ajustement possibles.
La standardisation directe (méthode de la population type) consiste à choisir une
population de référence dont on connaît la proportion de sujets pi dans chaque strate i. Le taux
standardisé direct (TSD) est alors la moyenne des taux spécifiques observés dans chaque strate ti,
pondérée selon la population de référence, c'est-à-dire, pour k strates,
TSD =
tpi
k
1i
i
avec
1p
k
1i
i
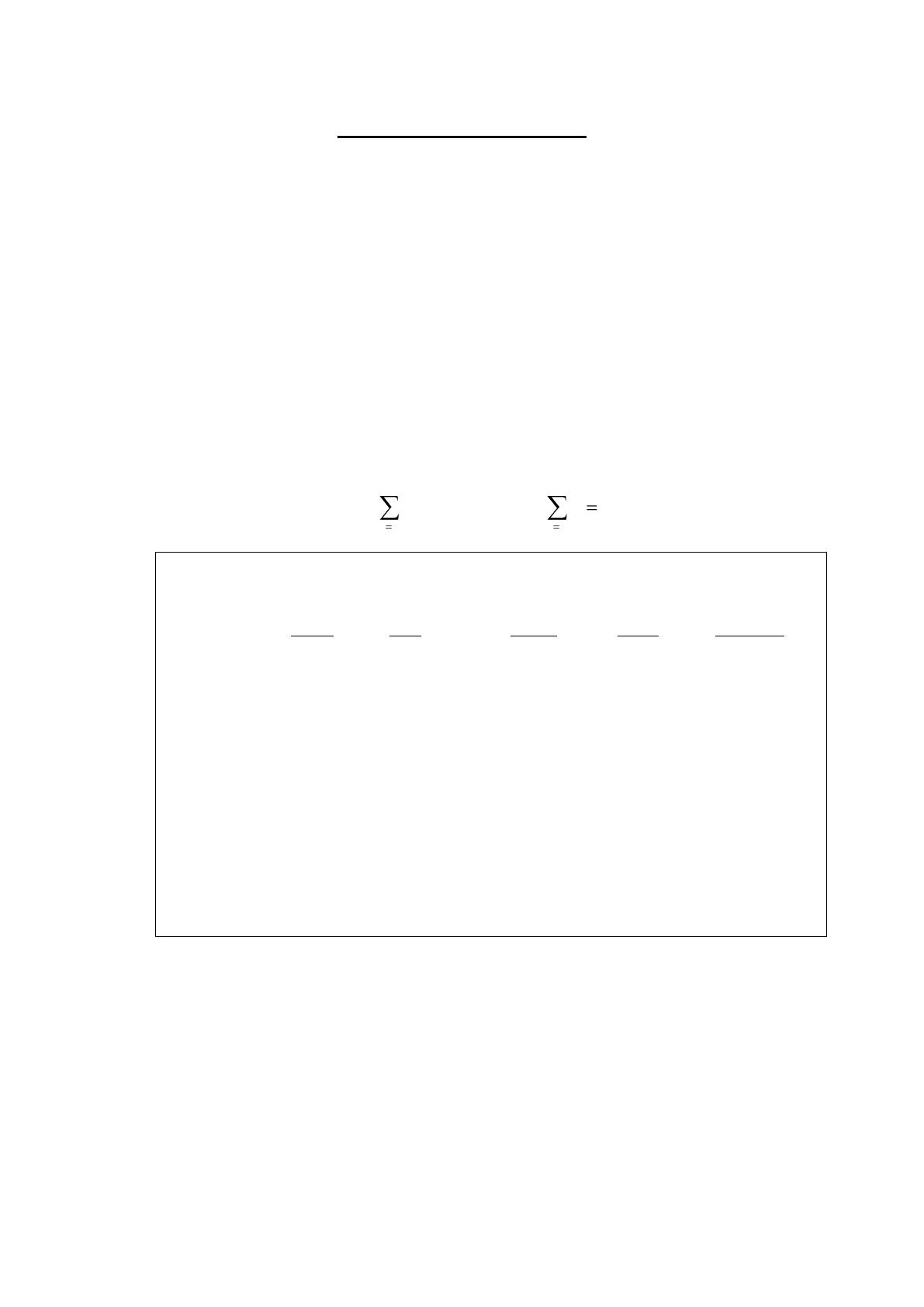
Classe Taux spécifiques Proportions par strate
rouge bleu rouge bleu référence
0 8,01 14,25 1,36 1,22 1,18
1-4 0,46 0,85 5,43 5,41 4,84
5-14 0,23 0,41 14,15 14,80 13,53
15-24 0,87 1,05 15,46 17,04 16,35
25-34 1,10 1,26 15,25 14,82 14,47
35-44 2,02 2,13 13,62 12,25 13,07
45-54 4,88 4,88 10,78 11,17 11,99
55-64 10,73 10,98 10,74 10,65 11,03
65-74 23,75 26,71 6,78 7,65 7,61
>75 90,58 95,36 6,43 4,99 5,93
——— ——— ———
∑ 100,00 100,00 100,00
Table 1. Taux de mortalité spécifiques de deux pays fictifs, rouge et bleu.
La table 1 présente des taux annuels de mortalité spécifiques par 1000 habitants de deux pays fictifs
appelés pays rouge et pays bleu, ainsi que les pourcentages correspondants des populations par
strate d’âge. Les taux de mortalité bruts pour les pays rouge et bleu sont respectivement
T = [(8,01 x 1,36) + (0,46 x 5,43) + …. + (90,58 x 6,43) ] / 100 = 9,86
et T = [(14,25 x 1,22) + (0,85 x 5,41) + …. + (95,36 x 4,99 ] / 100 = 9,42.
Les taux standardisés directs basés sur une population de référence pi sont eux, pour le pays rouge,