Rappel proba et Processus de Markov

1
Rappel de probabilités
P peut être définie par la connaissance des pi = P({ai}) qui sont
positifs et vérifient :
Si X est un sous ensemble de nombres réels :
Moyenne : , Variance :
Ecart type :
Exemple - Loi de Poisson de taux λ"
• E = {0,1, 2, ……. , n …….} avec
• Dans ce cas on démontre que EX= λ"

2
Variable aléatoire continue
X E = ou [a,b], ou [a, [, ou ] - , b]
Fonction densité de probabilité
f : E  avec
On a
Moyenne :
Variance :
Probabilité conditionnelle
Etant donné A et B deux sous ensembles de E.
On note par A (respectivement B) l’évènement
On définit p(A/B) la probabilité de A sachant que B s’est
réalisée par :

3
Exemple - Loi exponentielle
T variable continue positive :
Sa fonction densité :
Fonction de répartition :
Moyenne :
Variance :
On a la probabilité conditionnelle :
(λ est un paramètre à déterminé)
Processus de Markov
est une famille de variables aléatoires prenant
leurs états dans un même ensemble discret (fini ou non)
E = {E1, E2, …En, ….} et vérifiant les propriétés suivantes :
• Sans mémoire
P(Xt+τ=Ej / Xu=Ek avec u<t et Xt= Ei} = P(Xt+τ=Ej / Xt= Ei} =
Pij(t,τ)
• Homogène
La probabilité de transition Pij(t,τ) ne dépend pas de t
(temps de la transition) et s’écrit : Pij(τ).

4
Hypothèse
On suppose que pour Δt suffisamment petit on a :
Pij(Δt) = λijΔt + o(Δt) pour
o(Δt) représente une expression qui vérifie la propriété
suivante :
Ainsi, l’expression o(Δt) devient négligeable lorsque Δt tend
vers 0.
Le terme λij est appelé le taux de transition de l’état Ei vers
l’état Ej.
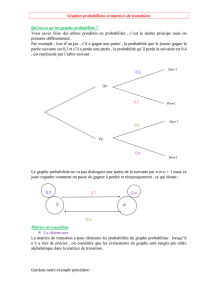
Graphe des probabilités de transition
Au processus de Markov on associe le graphe G=(X,U) défini par :
- X = {E1, E2, …, Ei,…} Ensemble des états du processus.
- U = {EiEj / λij>0} (les arcs correspondent à des taux de transitions
non nuls).
Exemple :
Xt représente l’état d’un guichet : E1 « occupé », E2 « non occupé ».
On suppose que : P12(Δt)=λΔt +o(Δt) et P21(Δt)=µΔt+o(Δt).
Le graphe associé :
E1 E2
λΔt
µΔt
1-µΔt
1-µΔt

5
Probabilité des états
Π(t) = (π1(t), π2(t), ……, πi(t) ….) représente la répartition des
probabilités des états au temps t, πi(t) = Prob(Xt=Ei).
Ainsi Π(0) représente la répartition des probabilités de la variable
X0.
Générateur infinitésimal du processus de Markov est défini par
la matrice carrée A = [aij] i,j =1,.., n avec :
On démontre que : Π’(t) = Π(t)A (1)
La relation (1) correspond à un système d’équations différentielles du
premier ordre avec la condition initiale Π(0).
Forte ergodicité , régime permanent
Le Processus de Markov sera dit fortement ergodique si :
On démontre alors que :
Et que cette limite est indépendante de la répartition initiale Π(0).
Π sera dite la répartition des probabilités des états en régime
permanent.
Condition suffisante : Si le graphe des probabilités de transition
est fini et fortement connexe, alors le processus de Markov
correspondant est fortement ergodique.