Correction PDF

Bac S Pondichéry 2012 Correction © http://labolycee.org
EXERCICE 1 : Laboratoires en impesanteur (6,5 points)
1
ère
partie : Le vol parabolique de l'airbus "A300 zéro G"
1.1. Le mouvement de l’avion, de masse m, est étudié dans le référentiel terrestre supposé
galiléen. Pendant la phase de chute libre, l’avion n’est soumis qu’à la force de pesanteur,
c’est-à-dire à son poids
P m.g
=
. La deuxième loi de Newton, appliquée au centre
d’inertie G de l’avion d’accélération
a
, donne :
P m.a
=
⇔
mg m.a
=
⇔
g a
=
En projection dans le plan xOz, avec l’axe Oz orienté vers le haut :
X X
Z Z
a g 0
a
a g g
= =
= = −
1.2.1. On a :
dv
a
dt
=
alors :
X
X
Z
Z
dv
a 0
dt
adv
a g
dt
= =
= = −
soit en primitivant
X
Z
v (t) Cte1
v
v (t) g.t Cte2
=
= − +
D’après les conditions initiales
0
v(0) v
=
donc
0
0
Cte1 v .cos
0 Cte2 v .sin
= α
+ = α
et finalement :
X 0
Z 0
v (t) v .cos
v
v (t) g.t v .sin
= α
= − + α
1.2.2.
Avec α = 47° , g = 9,8 m.s
−2
et v
0
= 600 km.h
−1
=
600 1000
3600
×
= 167 m.s
−1
, on a :
2
X
2
Z
v (t) 167 cos47 114 1,1 10
v
v (t) 9,8t 167 sin47 9,8t 122 9,8t 1,2 10
= × = = ×
= − + × = − + = − + ×
en conservant 2 chiffres significatifs.
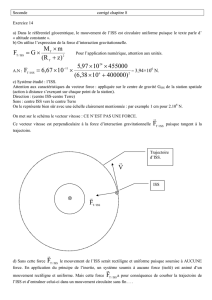
1.3.1.
Au somment S de la trajectoire, le vecteur-vitesse de l’avion est horizontal.
Ainsi v
Z
= 0 en S.
1.3.2.
Soit t
S
la durée de la phase ascendante, alors : v
Z
(t
S
) = 0 donc – g.t
S
+ v
0
.sinα = 0
Finalement :
0
S
v .sin
tg
α
= ;
S
600 1000 sin47
t3600 9,8
× ×
=×= 12 s.
Valeur non arrondie stockée en mémoire
La durée de la phase ascendante de chute libre de l’avion est d’environ 12 s.
1.4.1.
On a :
dOG
v
dt
=
donc
2
X
2
Z
dx
v (t) 1,1 10
dt
vdz
v (t) 9,8.t 1,2 10
dt
= = ×
= = − + ×
soit en primitivant
2
2 2
x(t) 1,1 10 .t Cte'1
OG
z(t) 4,9.t 1,2 10 .t Cte'2
= × +
= − + × +
Comme
3
0
OG(0) z .k 8,0 10 .k
= = ×
où
k
est le vecteur unitaire porté par l’axe Oz, il vient :
3
0 0 Cte'1
8,0 10 0 0 Cte'2
= +
× = + +
Finalement :
2
2 2 3
x(t) 1,1 10 .t
OG
z(t) 4,9.t 1,2 10 .t 8,0 10
= ×
= − + × + ×

1.4.2. On a : z
max
= z(t
S
) = − 4,9.t
S2
+ 1,2×10
2
.t
S
+ 8,0×10
3
z
max
= − 4,9×(12,438)
2
+ 1,2×10
2
×12,438
+ 8,0×10
3
z
max
= 8,76×10
3
m = 8,8 km. calcul effectué sans aucun arrondi intermédiaire
Cette valeur est bien compatible avec la valeur de 8,7 km fournie dans l’extrait du document
scientifique.
2
ème
partie : Caractéristiques du mouvement de la station ISS
2.1. La force
F
d’attraction gravitationnelle exercée par la Terre sur la station ISS est
appliquée sur la station et est orientée vers la Terre.
La norme de cette force est :
( )
T
2
T
m.M
F G.
R z
=+
2.2. La deuxième loi de Newton,
appliquée à la station ISS dans le
référentiel géocentrique donne :
F m.a
=
En prenant la norme de chaque
membre de l’égalité vectorielle il
vient : F = m.a
soit
( )
T2
T
m.M
G. m.a
R z =
+
et finalement :
( )
T
2
T
G.M
a
R z
=+
Comme
F m.a
=
, le vecteur-
accélération
a
est colinéaire et de
même sens ( m > 0 ) que
le vecteur
F
.
2.3.1. On a :
( )
2 2
T
v v
a
r R z
= =
+
et
( )
T
2
T
G.M
a
R z
=+
donc
( ) ( )
2T
2
TT
G.M
v
R z
R z
=
++
( )
2T
T
G.M
v
R z
=
+
finalement la norme du vecteur vitesse est :
( )
T
T
G.M
v
R z
=
+
(On ne garde que la solution positive).
2.3.2.
( )
11 24
3 2 3
6,67 10 6,0 10
v
6,4 10 3,5 10 10
−
× × ×
=× + × × = 7,7 ×10
3
m.s
−1
= 7,7 km.s
−1
.
en ayant converti les longueurs en mètres.
2.3.3. Le satellite a un mouvement circulaire et uniforme, de rayon R
T
+ z à la vitesse v.
La période de révolution T du satellite est telle que :
(
)
T
2 R z
vT
π +
=.
Donc :
(
)
T
2 R z
Tv
π +
=.
2.3.4.
(
)
3 2 3
3
2 6,4 10 3,5 10 10
T7,7 10
π × + × ×
=×= 5,5
×
10
3
s.
En 24 h soit 24
×
3600 = 86 400 s, la station ISS effectue
3
86400
5,5 10
×= 15,7 soit près de 16
révolutions chaque jour.
3
eme
partie : Comparaison :
Dans la station ISS, l’état d’impesanteur est permanent alors qu’il ne
dure que 25 secondes environ dans les vols paraboliques de l'airbus A300 Zéro-G.
F
a
1
/
2
100%