Corrigé gratuit du Bac Mathématiques spécialité Pondichéry 2015

Corrrigé du sujet de Baccalaurat S
Pondichery 2015
Spécialité
EXERCICE 1 (4 points) commun à tous les candidats
Partie A
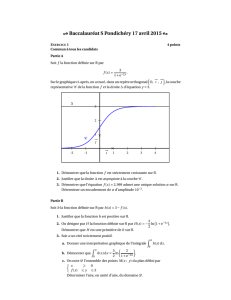
Soit f la fonction définie sur R par f(x)
  et la droite d’équation et la droite d’équation y
3.
1) Démontrer que la fonction f est strictement croissante sur R.
 Calcul de la dérivée de f(x) :
La fonction f est définie sur R, car son numérateur est non nul, et elle est dérivable.
La fonction f est de la forme f(x) 3. 
 ; sa dérivée sera de la forme f’(x)
3. 
avec u   et u’ -2 .
Donc f’(x) 3. 
  .
On a donc   f’(x)
 Signe de la dérivée f’(x) :
La fonction exponentielle est strictement positive sur R, donc la dérivée étant le quotient de deux fonctions
positives, elle est strictement positive sur R.
On en déduit que la fonction f est donc strictement croissante sur R.
2) Justifier que la droite  est asymptote à la courbe C.
 Détermination de la limite en  :
  0
Puis, par addition :
  1
Et par quotient :
 3
On a donc  0
On en conclut que la droite  d’équation y  3 est asymptote à la courbe C
3) Démontrer que l’équation f(x)  2,999 admet une unique solution α sur R.
Déterminer un encadrement de α d’amplitude 10-2.
 Détermination de la limite en  :
Puis, par addition :
Et par quotient :
 0
On a donc  0
Par composition,  0
Par composition,  

 Tableau de variation de f :
On a donc :
x
 α 
f'(x)
f(x)
3
0
La fonction f étant dérivable sur R, elle est continue et strictement croissante sur R.
D’après l’étude des limites et le tableau de variations, l’image de R par f est l’intervalle ]0 ; 3[.
Or λ  2,999 appartient à l’intervalle ] 0 ; 3[.
Donc, d’après le théorème des valeurs intermédiaires, f(x)  λ  2,999 admet une solution unique α sur
R.
 Encadrement de α :
A la calculatrice, en remarquant que
 f(4)  2,99899
 f(4,01)  2,99901
Partie B
Soit h la fonction définie sur R par h(x)  3 – f(x).
1) Justifier que la fonction h est positive sur R.
Dans la partie A, nous avons démontré que l’image de R par f est l’intervalle ]0 ; 3[.
Donc x R, 0 < f(x) < 3
-3 < - f(x) < 0
0 < 3 - f(x) < 3
Donc 0 < h(x) < 3
Donc la fonction h est positive sur R.
2) Démontrer que H(x)  
 ln(1  e -2x) est une primitive de h(x).
H est dérivable sur R, car les fonctions qui la composent le sont.
H(x) est de la forme 
 ln(u(x)), avec u(x)  1  e -2x, et u’(x)  -2e -2x.
H’(x) est de la forme 
.  .
Donc H’(x)  
 x 
H’(x)  
Or h(x) 3 - 
.
Donc H’(x)  h(x).
Donc H est bien une primitive de h sur R.
2,999
Alors 4 < α < 4,01

3) Soit a un réel positif.
a) Donner une interprétation graphique de l’intégrale 
 la fonction h est continue sur R, donc intégrable sur l’intervalle [0 ; a] (a>0)
 fonction h est positive sur R, donc en particulier sur [0 ; a] (question B. 1)
 On a h(x)   
 Donc l’intégrale 
 représente l’aire, en unité d’aire, délimitée par :
- les droites d’équation x  0 et x  a ;
- la droite  d’équation y  
- la courbe C
 représente l’aire hachurée sur la figure.
b) Démontrer que 
  H(a)- H(0)
 () 
 2
  ; or 
Donc 
c) On note D l’ensemble des points M(x ;y) du plan défini par x  
f(x)    3
Déterminer l’aire, en unité d’aire de D.
On travaille ici sur le demi-plan d’équation x  .
L’aire recherchée est l’aire du domaine compris entre :
 La droite  d’équation y3
 La courbe Cf
 Et le demi-plan d’équation x  
On a donc AD   
Or
  0
  1,
 Donc   
  2, et par composition et produit :  
Donc l’aire recherchée est AD  
.

EXERCICE 2 (4 points) commun à tous les candidats
Partie A
Soit (un) la suite définie par son premier terme u0 et, pour tout entier nature n, par la relation
un
1
aun b (a et b réels non nuls tels que a1).
On pose pour tout entier naturel n, vn un - 
1) Démontrer que la suite (vn) est géométrique de raison a.
vn
1
un
1 - 
aun b - 
a
a
a. vn
On en conclut que (vn) est géométrique de raison a et de 1er terme v0 u0 - 
2) En déduire que, si a appartient à l’intervalle]-1 ; 1[, alors la suite (un) a pour limite
.
 De la question 1) on peut écrire vn en fonction de n :
vn v0 . an
or vn un - 
 On en déduit :
un vn  
un v0 . an
 Etude de la limite :
Or si -1 < a < 1, alors 
 an
0
Donc 
 (v0 . an )
0
 Conclusion :
 un
 . La suite un converge vers 
Partie B
En mars 2015, Max achète une plante verte mesurant 80 cm. On lui conseille de la tailler tous les ans, au
mois de mars, en coupant un quart de sa hauteur. La plante poussera alors de 30 cm au cours des douze
mois suivants.
1) Quelle sera la hauteur de la plante en mars 2016 avant que Max ne la taille ?
Dès qu’il est rentré chez lui, Max a taillé sa plante, à laquelle il n’est resté que ¾ de sa hauteur. Sa
plante a donc poussé de 30 cm dans l’année, et mesure donc en mars 2016 :
80 

2) Pour tout entier naturel n, on note hn la hauteur de la plante, avant sa taille, en mars de l’année (2015+ n).
a) Justifier que, pour tout entier naturel n, h n+1 = 0,75 hn  .
Soit hn la taille de la plante l’année (2015 + n). Puisque Max coupe ¼ de sa hauteur, il reste ¾ de hn, c’est-
à-dire 0,75 hn, puis la plante gagne 30 cm.
On a donc    h n  0,75 h n  .
b) Conjecturer à l’aide de la calculatrice le sens de variations de la suite (hn).
Démontrer cette conjecture (on pourra utiliser un raisonnement par récurrence).
 En faisant tourner un programme qui calcule hn en fonction de n, on peut conjecturer que la suite est
strictement croissante.
 démonstration par récurrence que h n+1 > hn :
- initialisation :
h0  80, et h1  90, donc h 1 > h0.
La conjecture est vraie au rang 0
- hérédité :
On suppose la conjecture est vraie au rang n, et que h n+1 > hn.
Donc on a : 0,75 h n+1  > 0,75 hn ,
C’est-à-dire : h n+2 > h n+1.
La conjecture est donc vraie au rang n+1.
 La conjecture est vraie au rang 0 et est héréditaire. On en conclut que la suite (hn) est croissante.
  h n+1 > hn .
c) La suite (hn) est-elle convergente ? Justifier la réponse
 En faisant tourner le programme de la question b), on observe que la suite semble être majorée par 120.
Dans la partie A, nous avons étudié la suite (un) définie par son premier terme u0 et, pour tout entier nature n, par la
relation : un
1
aun b (a et b réels non nuls tels que a1).
Posons un hn ; a 0,75 ; b 30 et u0 h0 80.
Dans la question A. 2), nous avons démontré que la suite un (donc hn) converge vers 
Donc (hn) converge vers  120.
EXERCICE 3 (6 points) Commun à tous les candidats
Partie A : Étude de la durée de vie d’un appareil électroménager
Des études statistiques ont permis de modéliser la durée de vie, en mois, d’un type de lave-vaisselle par une variable
aléatoire X suivant une loi normale N(μ , σ²) de moyenne μ = 84 et d’écart-type σ. De plus, on a P(X  64) = 0,16.
La représentation graphique de la fonction densité de probabilité de X est donnée ci-dessous.