Chapitre 5 : Trigonométrie.

Chapitre 5 : Trigonométrie.
I - Cercle trigonométrique.
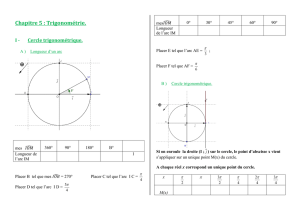
A ) Longueur d’un arc
mes 
360°
90°
180°
Β°
Longueur de
l’arc IM
l
Placer B tel que mes 
 = 270° Placer C tel que l’arc I C =
4
Placer D tel que l’arc I D =
4
5
mes
0°
30°
45°
60°
90°
Longueur
de l’arc IM
Placer E tel que l’arc AE =
3
;
Placer F tel que AF =
6
B ) Cercle trigonométrique.
Si on enroule la droite (I ;
j
) sur le cercle, le point d’abscisse x vient
s’appliquer sur un unique point M(x) du cercle.
A chaque réel x correspond un unique point du cercle.
x
2
2
3
4
4
2
4
3
M(x)

x
4
+ 27×2 π
-
2
-π
-
4
3
4
7
2
15
M(x)
Définition : Le cercle C ainsi gradué est un cercle trigonométrique.
2
est l’abscisse curviligne de J. …
Remarque : Si x est une abscisse curviligne de M alors tout réel de la
forme x + … avec k ∈ ℤ est une abscisse curviligne de M.
C ) Mesure d’angle en radian.
Définition : Soit M un point du cercle trigonométrique et x son abscisse
curviligne.
Mesure en radian de l’angle orienté (  : mes(  = x
Propriété : Les mesures en degrés et en radians, d’un angle géométrique,
sont proportionnelles.
x
0
2π
3π
5π
7π
π + 52×(2 π)
M(x)

II - Angle orienté de deux vecteurs non nuls
A ) Définition.
Soit C un cercle trigonométrique d’origine I.
Définition : Soit les points M et N d’abscisses curvilignes xm et xn.
);( ONOM
est un angle orienté de vecteurs.
mes
);( ONOM
= xn – xm.
Exercice : Donner les mesures d’angles en radians.
Remarque :
);( ONOM
désignera soit l’angle soit sa mesure.
Définition : Soit  et  deux vecteurs non nuls.
L’angle orienté des vecteurs  et  est celui des vecteurs unitaires
 où M et N sont des points du cercle trigonométrique tel que
et 
i.e. ( ;) =
Remarque : si α est une mesure de (
u
;
v
), alors
α + k2π (k ∈ ℤ) est aussi une mesure de (
u
;
v
)
On écrira (
u
;
v
) = α + k2π (k ∈ ℤ) ou bien (
u
;
v
) = α (2π) "modulo"
Définition : On appelle mesure principale d’un angle orienté de vecteurs
non nuls, la mesure en radians de cet angle qui appartient à ] – π ; π ]
Exemple : (
u
;
v
) = 
La mesure principale de (
u
;
v
) est
Car (
u
;
v
) = ………..=
mes
);( OEOI
=
mes
);( OJOE
=
mes
);( OJOH
=
mes
);( OEOJ
=

B ) Propriétés des angles orientés.
Angle nul : ( ; ) = 0 (2π)
Angle plat : ( ; ) = ( ; ) = π (2π)
Propriétés : k est un réel positif;  ,  et  sont trois vecteurs non nuls.
 ( ; ) = ( ;) + ( ;  ) (2π) (relation de Chasles)
 ( ; k ) = ( ; ) = (k ; ) (2π)
Conséquences :
 ( ; ) = - ( ; ) (2π)
 (- ; ) = ( ; - ) = ( ; ) + π (2π)
Démonstration : (à compléter)
( ; ) + ( ; ) = …… = ….. ( 2π) d’où
(- ; ) = ( ; ) + ( ; ) = ….. + ……. (2π)
Exemple 1 : ABCD est une rectangle
Déterminer ( ; )
Exemple 2 : ABC est une triangle équilatéral.
Compléter par les mesures :
( ; ) =
( ;  ) =
( ) = ( ; ) + π = 
 + π = 

III - FONCTIONS CIRCULAIRES (sinus et cosinus)
A ) Définition :
Soit M un point du cercle trigonométrique tel que x soit une mesure en
radian de l’angle orienté (
OMOI,
). Alors :
 cos(x) est l’abscisse de M dans le repère (O,
OJOI,
)
 sin(x) est l’ordonnée de M dans le repère (O,
OJOI,
)
Remarque : tan x =
x
x
cos
sin
pour x ≠
2
+ k π
B ) Tableau de valeurs
Compléter :
x
0
π
-2 π
2
2
2
3
2527 π
M(x)
cos(x)
sin(x)
C ) Propriétés
a) pour tout x réel , ≤ cos(x) ≤ ; ≤ sin(x) ≤
b) pour tout x réel [cos(x)] 2 + [sin(x)] 2 =
que l’on écrit : cos² x + sin² x =
Application au tableau de valeurs suivant :
x
0
6
4
3
2
M(x)
sin x
cos x
* Posons a le réel tel que a = cos (
4
) = sin (
4
)
En utilisant la propriété b), trouver la valeur de a.
* M1 est le point d’abscisse curviligne
3
.
Que dire du triangle OIM1 ?
H est le projeté orthogonal de M1 sur (OI).
Que dire de H ? En déduire cos(
3
).
En utilisant la propriété b), trouver sin(
3
).