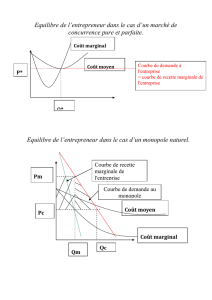
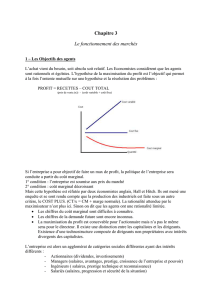
Introduction

1
1
Chapitre 5: Concurrence
imparfaite
Chapitres 11-15 dans le Perloff
2
Menu de ce chapitre
Apéro
Le monopole et ses effets sur le bien-être
Entrée
Concurrence monopolistique servi avec un potpourri
d’oligopole (concurrence à la Cournot, Betrand et
Stackelberg)
Dessert
Théorie des jeux avec de la crème chantilly
3
Introduction
Nous abandonons la concurrence parfaite
et nous étudions d’autres structures de
marché, càd:
• monopole
• concurrence monopolistique
• oligopole
4
Monopole
Un monopole, c’est une structure de marché
où seule une seule firme offre le bien
(production du monopole = production du
marché).
→un monpoleur ne peut pas considérer le prix
du marché comme donné, mais il est plutôt un
“faiseur de prix” (price setter).

2
5
Exemples
• Microsoft depuis les années 1990 sur le marché
des systèmes d’exploitation des ordis personnels
“Intel-compatible” – c’est quoi un marché?
• IBM dans les 1960s sur le marché des “mainframe
computers”
• Service postal suisse dans le marché du “non-
courier non-bulk mail delivery” en Suisse
• Les TL sur le marché des transports lausannois
• Services de cafét sur le campus à Dorigny
6
Maximisation du profit du monopoleur
Le monopoleur considère la demande du
marché comme donnée et décide de son prix
et de sa quantité:
càd: le monopoleur choisit le point sur la
courbe de demande qui maximise ses profits
)p(DQ s.c.
)Q(CpQmax Q,p
=
−=Π
7
Choisit-il le prix ou la quantité? Peu importe.
Supposons qu’il choisisse la quantité. Alors,
le prix est donné par la fonction de
demande inverse:
Maximiser les profits donne donc la
condition de premier ordre:
)()( 1QDQp − =
0)()()(' =
′
−+ QCQpQQp
8
La condition de deuxième ordre (CDO):
Si la CDO est satisfaite, alors la condition
d’optimalité est donnée par:
revenu marginal (Rm) = coût marginal (Cm)
C’est comme en concurrence parfaite avec une
différence importante: le revenu marginal du
monopoleur est plus petit:
0)()('2)('' <
′′
−+ QCQpQQp
ppQQp <+)('

3
9
La raison: si le monopoleur augmente la
quantité produite, il diminue le prix auquel il
peut la vendre sur le marché.
Donc, le monopoleur augmente son prix au
delà du cout marginal (pour un monopoleur,
diminuer la quantité, c’est augmenter le
prix!).
10
Comparison graphique
Marché en concurrence: Monopoleur:
p
qq+ 1
p1
Demand curve
AB
qQQ+ 1 Q
p1
p2
p
Demand curve
AB
C
11
Dérivation du prix optimal
0
AC
AVC
e
Demand
π
MC
MR
Q
p
12
La règle optimale en termes d’élasticités:
Rappel: l’élasticité prix est définie comme:
Donc la condition de premier ordre devient:
Q
p
dp
dQ
p== )(
εε
)
1
1()(
Q
p
dp
dQ
ppQ
dQ
dp
QC +=+=
′
)
1
1(
ε
+= p

4
13
En particulier:
Si la demande est partout très élastique ( est
proche de ), alors le monopoleur choisit une
quantité de sorte que le prix soit proche du coût
marginal: dans ce cas le monopoleur est proche
de la concurrence parfaite.
Si la demande est inélastique ( ), le prix est
beaucoup plus élevé que le coût marginal: le
monopoleur a beaucoup de pouvoir de marché.
ε
∞−
1≤ε
14
Observation:
Le monopoleur va choisir un point dans la
partie élastique de la demande.
Preuve:
Si , alors le revenu marginal est négatif.
Donc si la firme, réduit sa production (le prix
augmente), son revenu augmente. Comme
nécessairement les coûts baissent, le profit
de l’entreprise augmente.
1< ε
15
Markups:
En réarrangeant la condition de premier
ordre:
Cette formule montre que le prix du
monopoleur est un markup sur les coûts
marginaux, p = m*Cm, avec un facteur de
markup:
)(/11
)(
)( Q
QC
Qp
ε +
′
=
1
)(/11
1>
+
=Q m
ε
16
Exemple algébrique:
Demande linéaire D(p) = a - bp
Donc on peut obtenir:
Demande inverse: p(Q) = a/b – Q/b
Revenu marginal: Rm(Q) = a/b – 2Q/b.
Ceci est une droite qui a la même ordonnée à
l’origine que la demande inverse mais qui a
une pente deux fois plus élevée.

5
17
La condition de deuxième ordre: Dans le cas
linéaire c’est:
Cette condition est satisfaite si le coût
marginal ne baisse pas trop rapidement (et
en particulier elle est satisfaite si le coût
marginal augmente sur le domaine d’intérêt).
Plus généralement, notre théorie du
monopoleur fait du sens si les économie
d’échelles ne sont pas trop importantes par
rapport à la fonction de demande.
b/2)Q(C −>
′′
18
La perte sèche du monopoleur:
Est-ce que l’optimisation du monopoleur est
efficiente au sens de Pareto?
Non, car le prix du monopoleur est en-dessus
du coût margial.
L’argument en détail: Supposons le
monopoleur produit . On sait que le prix
sera: . Maintenant un
consommateur est prêt à payer ,
mais pas .
M
Q
)Q(Cm)Q(p MM >
)Q(Cmp M >
)Q(p M
19
Si le monopoleur vend à ce consommateur
seulement une unité à un prix plus petit que
, le monopoleur et le consommateur
gagnent à l’échange.
La raison de l’inefficacité est le fait que le
monopoleur ne peut pas faire une discrimination
des prix parfaite: si le monopoleur offre un prix
plus bas à un consommateur marginal (ce qu’il
aimerait faire), il doit offrir ce même prix aussi à
tous les autres consommateurs (infra-marginaux)
ce qui fait baisser le profit du monopoleur.
)Q(p M
20
La perte sèche du monopole: C + E
p
Demand
Q
MR
MC
pcB
D
C
E
MR= MC
A
pm
QmQc 0
em
ec