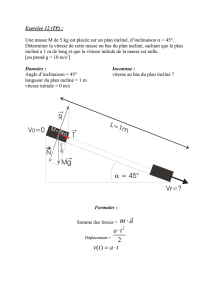
Le plan incliné : Lois de Newton et mouvement

Chapitre 2
Le plan incliné
Lorsqu’un corps glisse le long d’un plan incliné, il n’est pas en chute libre. Ce corps
est contraint de se déplacer le long du plan. Le corps ne chute donc plus verticale-
ment, mais il glisse le long de la pente du plan avec une accélération différente de
g(figure 2.1). Si l’accélération est constante, les équations du mouvement rectiligne
uniformément accéléré vues au chapitre 1 s’appliquent toujours. L’essentiel ici sera
donc de trouver une façon d’exprimer l’accélération d’un objet sur un plan incliné
pour pouvoir éventuellement décrire son mouvement.
Dans ce chapitre nous étudierons le mouvement d’un objet sur un plan incliné,
sans frottement et soumis à l’action de plusieurs forces. Ce sera l’occasion de présenter
les deux premières lois de Newton relatives au mouvement. Ces lois sont à la base de
la mécanique classique.
θ
Figure 2.1 – Direction de la chute sur un plan incliné.
13

14 Physique des mécanismes
2.1 Projection de l’accélération
Puisqu’un objet glissant sur un plan in-
θ
θ
g
g sinθ
Figure 2.2 – Projection de l’accélération sur
le plan incliné.
cliné ne peut accélérer verticalement, son
accélération sera plus petite que g. S’il
n’y a pas de frottement, son accélération
sera égale à la composante de gle long
du plan (figure 2.2.)
L’angle du plan sera toujours donné
par rapport à l’horizontale, ce qui nous
permet grâce à la géométrie de trouver
l’expression de l’accélération
a=gsin ◊.(2.1)
2.2 Les deux premières lois de Newton
La figure 2.3 présente un extrait des Philosophiae Naturalis Principia Mathematica de
Newton 1où il présente ses trois lois du mouvement. Les deux premières lois peuvent
se résumer ainsi :
Première loi ; si aucune force résultante ne s’exerce sur un corps, la vitesse
de ce corps ne peut pas varier. Son accélération est nulle.
Seconde loi ; la force résultante exercée sur un corps est égale au produit de
la masse de ce corps et de son accélération.
˛
Fr´esultante =m˛a(2.2)
1. Publié pour la première fois à Londres en 1687, ce livre est considéré comme l’un des plus
important de l’histoire. Il a été traduit pour la première fois en français par Émilie du Châtelet et
publié par Voltaire en 1756, sous le titre Principes mathématiques de philosophie naturelle.

Chapitre 2. Le plan incliné 15
Figure 2.3 – Extrait des Principia de Newton (1643–1727) traduit par Mme du
Châtelet (source Bibliothèque Nationale de France).

16 Physique des mécanismes
2.3 L’application de la deuxième loi de Newton
Un exemple simple d’application de la deuxième loi de Newton est présenté à la figure
2.4 où l’on doit trouver l’accélération des deux masses Met m. On suppose que la
corde reliant les deux masses est elle-même sans masse et qu’elle ne s’étire pas. Par
conséquent, la grandeur de l’accélération de Mdoit être égale à celle de m
aM=am=a. (2.3)
De plus selon la formulation de la deuxième loi, il faut considérer la force résul-
tante sur chacune des masses. Pour Mil n’y a que la tension Tdans la corde
FM=T=Ma. (2.4)
Quant à m, deux forces agissent sur elle, la gravité et la tension dans la corde.
Puisque ces deux forces sont en direction opposée, elles se soustraient. La résultante
des forces sur mest donc
Fm=mg ≠T=ma. (2.5)
La tension est partout la même dans la corde. On peut donc isoler Tdans l’équa-
tion (2.5) et remplacer l’expression ainsi obtenue dans l’équation (2.4) pour trouver
la valeur de a
mg ≠ma =Ma
Ma+ma =mg
a(M+m)=mg
a=m
M+mg. (2.6)
Puisque la force est le produit de la masse et de l’accélération, l’unité de la force
est le kg·m/s2qu’on définit comme étant le Newton (N)
1kg·m/s2=1N.(2.7)

Chapitre 2. Le plan incliné 17
M
m
T
T
mg
Figure 2.4 – Un bloc sur une surface lisse est tiré par un deuxième bloc suspendu.
 6
6
 7
7
 8
8
 9
9
 10
10
1
/
10
100%