PROPORTIONNALITE : applications I Vitesse et Débit v= d t

PROPORTIONNALITE : applications : 1
PROPORTIONNALITE : applications
I Vitesse et Débit
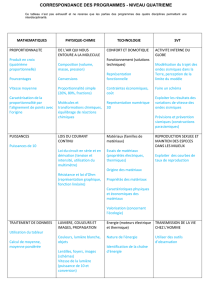
Vitesse Débit
La vitesse (moyenne) est le coefficient de
proportionnalité entre le temps et la distance.
v= d
t
ou
avec v (vitesse), d (distance) t (temps)
Attention aux unités !
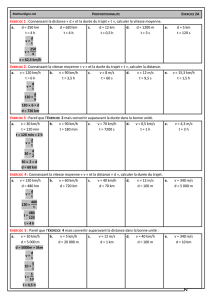
Exercice 1 : Vitesse
Un automobiliste a une vitesse moyenne de 105 km/h sur autoroute.
a. Il effectue le trajet en 2 h 40 min. Quelle distance a-t-il parcourue ?
b. Il doit parcourir à la même vitesse un trajet de 140 km. Quel temps mettra-t-il ?
Exercice 2 : Paradoxe de la vitesse
a. Antoine et Paul parcourent à bicyclette le trajet entre Angers et Segré, soit 40 km, en 1h20.
Quelle est la vitesse moyenne ?
b. Antoine effectue le retour à une vitesse de 15km/h. Quelle est sa vitesse moyenne sur l’aller et le
retour?
c. Paul revient en automobile à la vitesse de 60 km/h. Quelle est sa vitesse moyenne sur l’aller et le
retour ?
Exercice 3 : Débit
a. Un évier se remplit en 40s avec un débit de 15 l /min. Quelle est sa contenance en l et en cm
3
?
b. Avec un même robinet, combien de temps faut-il pour remplir une baignoire de 0,24 m
3
?

PROPORTIONNALITE : applications : 2
c. Soit un bassin rectangulaire de longueur 2 m, de largeur 80 cm et de profondeur 50 cm. On le remplit
avec un débit de 20 l /min. Combien de temps faut-il ?
d. Au cours de l’été il est tombé 12 mm d’eau. Combien de litres sont tombés sur un terrain rectangulaire
de dimension 25 m sur 2 dam ?
II Masse volumique et densité
Ex : 1,6 m
3
de laiton a une masse de 13 440 kg. Calculer sa masse volumique et sa densité.
Définition de la masse volumique :
Définition de la densité d’un corps :
III Echelle
L’échelle est le coefficient de proportionnalité entre la dimension réelle et la dimension de la carte (ou de
la maquette, ou de la photo)
Echelle = dimension.sur.la.carte
dimension.réelle (avec les dimensions dans la même unité!)
Exercice :
a. Sur une carte à l’échelle 1/25 000, 2 villes sont séparées de 12,5 cm. Quelle est la distance réelle entre
ces 2 villes en km.
b. Les dimensions d’un stade rectangulaire sont 120 m et 50 m. Quelles sont les dimensions obtenues
pour une maquette à l’échelle 1/400.
c. Quelle est l’échelle si la distance entre 2 villes est 250 km en réalité et 5 cm sur la carte ?

PROPORTIONNALITE : applications : 3
IV Partage proportionnel et inversement proportionnel
Partage proportionnel
Soit une somme S=1500 euros.
a. Si cette somme est partagée entre 3 personnes proportionnellement à 1, 3 et 4, on obtient
respectivement pour chaque personne :
b. Si cette somme est partagée entre 3 personnes respectivement à leur nombre d’enfants, 2, 3 et 5, on
obtient respectivement pour chaque personne :
Partage inversement proportionnel
a. Si une somme de 1700 euros est partagée entre 3 personnes inversement proportionnellement à 1, 2 et
5, on obtient respectivement pour chaque personne :
b. On souhaite répartir une prime de 1650 euros à 3 employés inversement proportionnellement au
nombre de jours d’absence : 2 5 et 8.
Exercice :
Trois employés sont licenciés et touchent une prime proportionnellement à leur ancienneté, 4 ans, 10 ans
et 20 ans. Le plus ancien touche une prime de 12 000 euros. Combien touchent les autres employés.
Double proportionnalité :
Pour construire un parking de 500 m² avec 4 employés, il faut 5 jours. Combien faut-il de jours pour
construire un parking de 200 m² avec 2 employés ?