géométrie CRPE

La géométrie au CRPE
Tout d’abord, il importe de bien connaître les propriétés de chacune des figures. Ensuite, pour démontrer
une affirmation, il suffit d’avoir un raisonnement cohérent et suivre un raisonnement logique.
Ainsi, si vous souhaitez démontrer que l’on a telle ou telle figure, il faut faire appel à ses propriétés
spécifiques. Il est, de plus, extrêmement important de connaître les conditions suffisantes pour affirmer que
cette figure est CE polygone. Cela vous évitera de vous embrouiller avec des explications confuses qui ne
vous feront que perdre du temps.
Les propriétés des figures
Droites
Si deux droites sont parallèles à une même troisième, alors elles sont parallèles entre elles.
Si deux droites sont perpendiculaires à une même troisième, alors elles sont parallèles entre elles.
Si deux droites sont parallèles, et si une troisième droite est perpendiculaire à l’une, alors elle est
perpendiculaire à l’autre.
Si deux droites sont parallèles et si elles ont un point commun, alors elles sont confondues (c’est à dire qu’il
s’agit en réalité de la même droite)!
Médiatrice
La médiatrice d’un segment est la droite qui passe par le milieu de ce segment et qui lui est perpendiculaire
Si un point est sur la médiatrice d’un segment, alors il est équidistant des extrémités de ce segment
Si un point est équidistant des extrémités d’un segment, alors il est sur la médiatrice de ce segment
Bissectrice
La bissectrice d’un angle est la demi-droite qui partage cet angle en deux angles adjacents de même
mesure.
Si un point est sur la bissectrice d’un angle, alors il est équidistant des côtés de cet angle.
Si un point situé à l’intérieur d’un angle est équidistant des côtés de l’angle, alors il est sur la bissectrice de
cet angle
TRIANGLES :
Si M est un point du cercle de diamètre [AB], alors le triangle AMB est rectangle en M
Les 3 bissectrices sont concourantes en 1 point = centre du cercle inscrit.
Les 3 médiatrices sont concourantes en 1 point = cercle circonscrit.
Les 3 médianes sont concourantes en 1 point = centre de gravité
Dans un triangle équilatéral toutes les droites remarquables sont confondues.
Dans un triangle rectangle, le centre du cercle circonscrit est le milieu de l’hypoténuse.

Théorème des milieux
Dans le triangle ABC, si J est le milieu de [AC] et si K est le milieu de [BC], alors (JK)//(AB
Réciproque
Dans le triangle ABC, si J est le milieu de [AC] et si K est un point de [BC] tel que (JK)//(AB) alors K est le
milieu de [BC) et JK = ½ BC
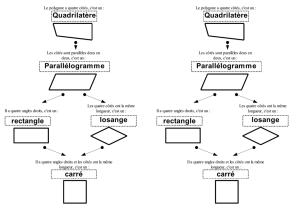
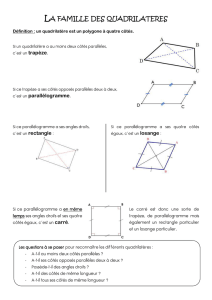
QUADRILATERES
Le parallélogramme est un quadrilatère dont les côtés sont opposés 2 à 2
Propriétés
(AB)//(DC) et (AD)//(BC)
AB=DC et AD=BC
Les diagonales se coupent en leur milieu
Les angles opposés ont la même mesure :
Aire = a x h
Le rectangle est un quadrilatère ayant 3 angles droits, ou c’est un parallélogramme ayant 1 angle droit.
Propriétés
(AB)//(DC) et (AD)//(BC)
AB=DC et AD=BC
Les diagonales se coupent en leur milieu et on même longueur
Les 4 angles = 90°
Aire = L x l
Le losange est un quadrilatère ayant tous ses côtés de même mesure. Ou le losange est un
parallélogramme ayant 2 côtés consécutifs de même mesure.
Propriétés
(AB)//(DC) et (AD)//(BC)
AB=BC=CD=DA
Les diagonales se coupent en leur milieu et sont perpendiculaires.
Aire AC x BD/2

Le carré est un losange ayant un angle droit. Ou le carré est un rectangle ayant 2 côtés consécutifs de
même mesure.
Propriétés
Il possède toutes les propriétés du losange et du rectangle
Aire = côté x côté
Le trapèze est un quadrilatère ayant 2 côtés parallèles.
Propriétés
Aire= (b+B)*h/2
Si les 2 côtés // ont également même mesure, alors la figure est un parallélogramme.
LES 2 SYMETRIES
La symétrie centrale : M’ est le symétrique de M par rapport à I si I est le milieu de [MM’]
Propriétés
La symétrie centrale conserve : les longueurs, l’alignement, les directions, le parallélisme, les angles.
La symétrie axiale : M’ est le symétrique de M par rapport à D si D est la médiatrice de [MM’]
Propriétés
La symétrie axiale conserve : les longueurs, l’alignement, direction quand la droite initiale est parallèle à la
droite de la symétrie, le parallélisme, les angles, les aires.