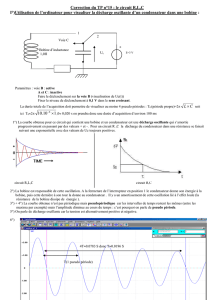
Pour calculer la valeur pratique des accélérations, nous

Guignet Marianne
Grebille Arnaud
TP1 21/03/07
Manipulation n°2
Changement de référentiel, lois de Newton
Objectifs du TP :
Le but de ce TP est de vérifier les lois de la dynamique pour différents types de
mouvements et pour un système à deux corps. Nous allons donc procéder à 3 manipulations
pour vérifier certaines lois concernant :
-un mouvement rectiligne à vitesse uniforme.
-deux mouvements rectilignes uniformément accélérés.
-le mouvement de deux mobiles accolés.
Matériel utilisé :
 1 caméra, zoom et focus automatique.
 1 repère en papier
 2 mobiles autoporteurs
 un ordinateur (logiciel utilisés : Excel, Cineris et Aviméca)
I- Exercice préliminaire :
Nous allons utiliser les deux formules suivantes pour obtenir
g
g
V
V'
et
g
g
V
V
2
2
'
Avec dans notre cas
i
RVV 
0
0
;
i
RVGV 
0
)(
et
gG VAV 22 )( 
On a donc ( avec m=m1=m2) :
Soit le rapport
iig
iig
VV
mm m
V
VV
m
m
V
3
2
2
2
'
2
1
*2
ig
iig
V
m
m
V
VV
mm m
V
9
1
3
'
4
1
)2(
2
2
2
2
2
2
9
4
'
2
2
g
g
V
V
0
00
21
2
)( R
RV
mm m
GV 
0
0
2
21
2
1)(
)2( RG V
mm m
AV 

II- Etude d’un mouvement rectiligne uniforme
Nous avons étudié un mouvement rectiligne uniforme à l’aide d’une séquence vidéo préenregistrée
sur le logiciel Cinéris. Nous avons donc appris à nous servir du logiciel (étalonnage, cadre de travail,
paramétrage).
Après un traitement de la vidéo par le logiciel, nous avons observé, à l’aide l’onglet « graphique » que
la trajectoire du mobile était rectiligne (obtention d’une droite).
Grâce au logiciel AviMéca2, nous avons évalué la précision des mesures de (x1 ; y1) à un pixel de
l’image. Nous avons ainsi trouvé une sensibilité horizontale de 1,35mm/pixels et une sensibilité
verticale de 1,32mm/pixels. Cette incertitude peut expliquer certains écarts entre la valeur théorique et
pratique lors des expériences.
Nous avons transféré les coordonnées de chaque point (x1;y1) ainsi que les temps correspondants sous
Excel. Le logiciel a calculé automatiquement les vitesses horizontales et verticales et la norme v de la
vitesse à l’aide des formules :
2
2
2
2
2
2
2
2
2
1
'
2
1
'
nn
nn
nn
nn
n
nn
nn
nn
nn
n
tt yy tt yy
y
tt xx tt xx
x
ainsi
2
1
2
11 'yxV 
Ensuite nous avons tracé le graphe et la droite de tendance sous Excel, l’équation de la droite est y=-
0,010x+0,345, cela montre que la vitesse du mobile est constante aux erreurs de manipulation près. En
effet, les frottements étant toujours légèrement présent, la vitesse décroît très légèrement (pente de la
droite négative).
norme de la vitesse en fonction du temps
y = -0,0108x + 0,3451
R2 = 0,1944
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,00E+00 1,00E-01 2,00E-01 3,00E-01 4,00E-01 5,00E-01 6,00E-01 7,00E-01 8,00E-01 9,00E-01 1,00E+00
temps (s)
Vitesse (m/s)
v
Linéaire (v)
La vitesse du mobile étant quasiment constante, le mouvement du mobile est donc uniforme (vitesse
moyenne=0.340m/s.
Ainsi nous pouvons conclure que le mouvement est rectiligne uniforme.

III- Etude du mouvement rectiligne accéléré
Nous avons étudié l’accélération et la vitesse de deux mobiles relié chacun à une masse par
l’intermédiaire d’un fil et d’une poulie sur une table à coussin d’air.
1) Etude de la vitesse et de l’accélération des mobiles :
Nous avons tout d’abord calculé les valeurs théorique des accélérations en fonction de la constante de
gravitation g (on prends g=9 ,8) et des masses m1 et M1 est :
g
Mm m
athéorique 
Soit
²/469.08.9
38766
38
1sma 
²/689.08.9
58766
58
2sma 
Pour calculer la valeur pratique des accélérations, nous avons préalablement pesé les mobiles et les
tractions.
Mobile 1
Mobile 2
Traction1
Traction 2
756 g
766 g
38 g
58 g
Nous avons ensuite fait l’acquisition vidéo de la manipulation (montage, étalonnage, paramétrage)
puis avons laissé Cineris traiter la vidéo.
Nous avons transféré les données (t ; x1 ; y1 ; x2 ; y2) dans Excel afin d’obtenir les courbes des
vitesse v1, v2 en fonction du temps. Ainsi la dérivée des équations des droites de tendance nous a
permis d’obtenir les accélérations (coefficients directeurs des droites) des deux mobiles lors de
l’expérience.
vitesses de a1 et a2 en fonction du temps
y = 0,4633x - 0,0436
R2 = 0,9935
y = 0,6512x - 0,0685
R2 = 0,9953
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
0,00E+00 1,00E-01 2,00E-01 3,00E-01 4,00E-01 5,00E-01 6,00E-01 7,00E-01 8,00E-01
temps (s)
vitesse (m/s)
v1
v2
Linéaire (v1)
Linéaire (v2)
On observe que la vitesse augmente proportionnellement par rapport au temps ce qui montre que les
mobiles ont un mouvement rectiligne uniformément accélérés.

Vitesse relative de A2 en fonction du temps
y = 0,0081x - 0,0056
R2 = 0,9774
0
0,02
0,04
0,06
0,08
0,1
0,12
0 2 4 6 8 10 12 14 16
temps (s)
vitesses relative de A2 (m/s)
Série1
Linéaire (Série1)
Tableau récapitulatif des accélérations : (en m/s²)
Valeur mesurée
Valeur théorique
Mobile 1
0,463
0,469
Mobile 2
0,651
0,689
La comparaison des valeurs expérimentales et théoriques semble proche. La faible erreur remarquée
provient probablement de la sensibilité du logiciel et des erreurs de manipulation.
2) Etude de la vitesse du mobile M2 relativement à M1
Excel calcule la vitesse relative de A2 par rapport à A1 à l’aide des coordonnés relative de A2 par
rapport à A1 puis en calculant la norme de la vitesse en utilisant les même formules que dans la partie
II.
On remarque que cette
vitesse relative évolue de
façon proportionnel au
temps se qui est était tout
à fait prévisible en
observant le graphe
précédant des vitesses de
A1 et A2.
Enfin, lorsque l’on
compare la vitesse relative
calculée par Excel à celle
que l’on obtient en
soustrayant V1 et V2, on
observe quelques très
légers décalages qui
peuvent être expliqués par
un nombre de chiffres
significatif insuffisant lors
des différents calculs.
IV) Etude du mouvement de deux mobiles accolés
1) Etude de la vitesse du centre de gravité
Après avoir accolé deux mobiles A1 et A2, on les lance par l’intermédiaire d’un propulseur
(positionné sur le mobile 2)et on étudie le comportement du centre de gravité du système.
Ainsi, après acquisition et traitement des données par Cinéris, nous obtenons les coordonnées du
mouvement des centres de gravité des deux mobiles (x1 ; y1 ; x2 ; y2) ainsi que les temps
correspondants.

On transfert les données sous excel qui calcule automatiquement les coordonnées du barycentre (xG ;
yG) ainsi que ses vitesses projetés x' et y' et la norme de sa vitesse.
vitesse de g en fonction du temps
y = -0,0093x + 0,2331
R2 = 0,4407
0
0,05
0,1
0,15
0,2
0,25
0,00E+00 2,00E-01 4,00E-01 6,00E-01 8,00E-01 1,00E+00 1,20E+00 1,40E+00 1,60E+00
temps (s)
vg (m/s)
vG
Linéaire (vG)
Nous remarquons que le norme de la vitesse du barycentre G est quasiment constante. Elle ne diminue
que très légèrement à cause des frottements qui sont encore présent malgré l’utilisation d’une table à
coussin d’air.*
On peux calculé la vitesse initial Vo de A2 à l’instant initial grace à la formule :
0
21
2
)( v
mm m
Gv 
Ainsi la vitesse moyenne de Vg étant de 0.22m/s et les mobiles m1 et m2 ayant des masses de 751g,
nous en déduisons que la vitesse V0 est de : 0.22*( 2*751/751)= 0.44m/s