symboles electriques utilisables dans word

Correction du TP n°15 : le circuit R,L,C
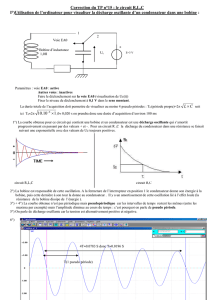
I°)Utilisation de l’ordinateur pour visualiser la décharge oscillante d’un condensateur dans une bobine :
Paramètres : voie B : active
A et C : inactive
Faire le déclenchement sur la voie B (visualisation de Uc(t))
Fixer le niveau de déclenchement à 0,1 V dans le sens croissant.
La durée totale de l’acquisition doit permettre de visualiser au moins 4 pseudo périodes : T0 (période propre)=2
CL
soit
ici T02
110.10 6
,0 0,020 s on prendra donc une durée d’acquisition d’environ 100 ms
1°) La courbe obtenue pour ce circuit qui contient une bobine et un condensateur est une décharge oscillante qui s’amortie
progressivement en passant par des valeurs + et -. Pour un circuit R ,C la décharge du condensateur dans une résistance se faisait
suivant une exponentielle avec des valeurs de Uc toujours positives.
circuit R,L,C circuit R,C
2°) La bobine est responsable de cette oscillation. A la fermeture de l’interrupteur en position 1 le condensateur donne son énergie à la
bobine, puis cette dernière à son tour la donne au condensateur . Il y a un amortissement de cette oscillation lié à l’effet Joule (la
résistance de la bobine dissipe de énergie ).
3°) + 4°) La courbe obtenue n’est pas périodique mais pseudopériodique car les intervalles de temps restent les mêmes (entre les
maxima par exemple) mais l’amplitude diminue au cours du temps : c’est pourquoi on parle de pseudo période.
5°) On parle de décharge oscillante car la tension est alternativement positive et négative.
6°)
Voie C
E=3 V
Bobine d’inductance
1,0H
1
+
Uc
2
4T0.0783 S donc T0.0196 S
T(1 pseudo période)

7°) Expérimentalement on trouve une pseudo période de T 0.0196 s (en mesurant 4 pseudo périodes puis en faisant la moyenne).
8°) Cette valeur est très proche de la période propre d’un circuit L ,C qui vaut 0.020 s. Remarquons d’ailleurs que la résistance de la
bobine entraîne un amortissement peu important sur le signal (Rbobine  12  voir TP n°14).
II°) Influence de différents paramètres sur la pseudo période :
1°) Influence de la tension E du générateur : Quand on modifie la tension aux bornes du générateur la pseudo période ne varie
absolument pas, on trouve toujours T 0.0196 s .
2°) +3°)
L=1H
L=1H
L=0,5H
C=10 F
C=1 F
C=10 F
T0 ,0196 s
T0 ,0061 s
T0 ,0138 s
T0 0,0198 s
T0 0,0063 s
T0 0,014 s
En regardant ce tableau on peut dire que la pseudo période dépend de L et C : quand L augmente la pseudo période augmente, il
en est de même quand C augmente (La pseudo période augmente).
4°) En augmentant la résistance du circuit on constate que la valeur de la pseudo période reste inchangée, par contre la
résistance joue sur l’amplitude de la courbe. Plus la résistance augmente plus l’amortissement devient important.
Pour une valeur de R supérieure à environ 270  on passe d’un régime pseudopériodique à un régime apériodique (il n’y a plus
d’oscillations). RC 270  est une résistance critique : c’est la dernière valeur de la résistance pour laquelle on a encore une
oscillation.
III°) Etude énergétique :
1°) A la date t=T/4 s la tension aux bornes du condensateur est au maximum elle vaut 2,24 V donc l’énergie emmagasinée par le
condensateur est au maximum car Ec=
)(
2
1tCUC
.
2°) Voir cliché ci-dessous.
3°)+4°) i=
dt
dU
C
dt
dq C
. Quand la courbe de Uc =f(t) passe par l’origine la dérivé
dt
dUc
est une droite quasi verticale donc
l’énergie emmagasinée par la bobine est au maximum car Ec=
)(
2
12tLi
=
22 )
)(
(
2
1dt tdU
LC C
5°) Voir cliché ci-dessous : (la suite sur la 3ième feuille).
6°) ET(énergie totale dans le circuit)= Ec (condensateur) + Eb (ou Em : énergie dans la bobine).
En regardant la courbe de ET (ci-dessous en jaune) on voit qu’il n’y a pas conservation de l’énergie totale dans le circuit, cette
dernière s’amortit à cause de l’effet joule lié à la résistance totale du circuit.
Uc=f(t) pour un circuit RLC (montage du I°)
-2,50E+00
-2,00E+00
-1,50E+00
-1,00E+00
-5,00E-01
0,00E+00
5,00E-01
1,00E+00
1,50E+00
2,00E+00
2,50E+00
0,00E+00 2,00E-02 4,00E-02 6,00E-02 8,00E-02 1,00E-01 1,20E-01
t (s)
Uc (V)

Evolution des différentes formes d'énergies pour un circuit RLC au cours du temps
-5,00E-06
0,00E+00
5,00E-06
1,00E-05
1,50E-05
2,00E-05
2,50E-05
3,00E-05
0,00E+00 2,00E-02 4,00E-02 6,00E-02 8,00E-02 1,00E-01 1,20E-01
t(s)
E (J)
Ec (J) (énergie du
condensateur
Eb (J) (énergie de la bobine)
Et=Ec+ Eb (énergie totale)