document élève - Académie de Nancy-Metz

Modélisation de l’évolution d’une population.
Soit P(t) l’effectif d’une population à l’instant t, t appartenant à l’intervalle
;0
.
A. Loi de Malthus.
Si l’on suppose que pour une petite durée
dt
, la variation
dP
de
P
est proportionnelle à
dt
et à
P
, on
a alors :
kPdtdP 
ou
kP
dt
dP 
.
1. Démontrer que dans ces conditions
kt
ePtP )0()( 
.
2. Quel est le sens de variation de
P
si
k
>0, si
k
<0 ? Quelle est dans chacun de ces cas la
limite de
)(tP
lorsque t tend vers + ?
3. Tracer la courbe représentative de P en prenant P(0)=1 et pour les valeurs suivantes de k :
k=0,1 ; k=1,5 et k=-0.2.
4. Pourquoi ce modèle d’évolution d’une population n’est-il pas pertinent pour t grand ? *
B. Equation logistique de Verhulst.
Le mathématicien belge Verhulst propose, vers 1840, le modèle suivant d’évolution d’une
population :
)( PmaP
dt
dP 
( a et m sont des constantes positives.)
1. Déterminer les solutions constantes de cette équation différentielle.
2. Déterminer le signe de
)0'(P
selon que 0<P(0)<m ou m<P(0). Dans la suite on ne
cherchera que les solutions telles que P(t)>0 pour tout t.
3. Par la méthode d’Euler tracer une courbe approchée de la solution de cette équation
différentielle dans les cas suivants :
a) a=0,1 ; m=1 et P(0)=2.
b) a=0,1 ; m=2 et P(0)=1.
4. Résolution de l’équation différentielle
)(' PmaPP
. On définit la fonction y telle que
)(
1
)( tP ty 
.
a. Montrer que y est solution de l’équation différentielle
amyay 
.
Résoudre celle-ci.
b. En déduire que
amt
Ce
m
tP  1 )(
où
)0( )0( PPm
C
.
5. Etudier et représenter la fonction P ainsi définie dans les deux cas suivants :
a) a=0,1 ; m=1 et P(0)=2.
b) a=0,1 ; m=2 et P(0)=1.
6. Comparer les résultats obtenus dans les questions 3 et 5. A votre avis que représente le
paramètre m de l’équation logistique ? Et le paramètre a ?

C. Exemples en écologie fondamentale et appliquée
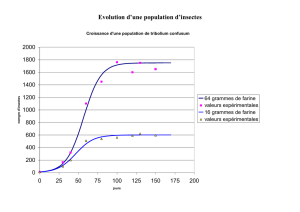
Croissance d'une population de tribolium confusum
0
200
400
600
800
1000
1200
1400
1600
1800
2000
025 50 75 100 125 150 175 200
jours
nomgre d'insectes
64 grammes de farine
valeurs expérimentales
16 grammes de farine
valeurs expérimentales
1°) Pour 64 grammes de farine on a relevé expérimentalement les données suivantes :
jours
population
0
10
30
165
40
320
60
1100
80
1450
100
1760
120
1600
130
1750
150
1650
Et on a modélisé la croissance de la population par la fonction
t
e
tf 09,0
1651 1750
:
.
Avec un grapheur représenter dans un même repère les données expérimentales et la fonction f. Ce
modèle vous parait-il pertinent ? Quel est le nombre maximum d’insectes que l’on peut prévoir selon ce
modèle ?
2°) Pour 16 grammes de farine on a relevé expérimentalement les données suivantes :
0
10
30
100
40
200
60
510
80
540
100
560
120
590
130
620
150
595
Déterminer une fonction P modélisant de façon satisfaisante l’évolution de cette population d’insectes.

Croissance de la population de moutons en Tasmanie
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
1830 1840 1850 1860 1870 1880 1890 1900 1910 1920 1930 1940
années
nombre de moutons en milliers
courbe réelle
courbe théorique