iii. etude des energies de l`oscillateur au cours du mouvement

P11 : Energie d’un système élastique
Objectif : faire une étude énergétique d’un système oscillant constitué de 2 ressorts et d’un solide S
I. DISPOSITIF ETUDIE
1. Présentation
Un solide S de masse m=125g est posé sur un banc à coussin d’air. Ce solide est maintenu en équilibre entre deux
ressorts identiques horizontaux, on note Go sa position d’équilibre.
On écarte le solide S de cette position d’équilibre, il se met à osciller avec une période To. En choisissant Go l’origine
de l’axe des abscisses, on note x la position du centre d’inertie G.
2. Principe de l’acquisition
Le centre d’inertie G du solide S est lié à une tige métallique dont l’extrémité est le point A qui trempe dans
une solution de sulfate de cuivre.
Le milieu de la cuve est repéré par le point O, il coïncide avec la position d’équilibre Go du solide S. La position du
point A (par rapport au point O) est proportionnelle à la tension u=UOA. L’enregistrement de cette tension au cours du
temps à l'aide d’une interface d'acquisition (boîtier Bora avec Synchronie) permet de suivre la position du centre
d’inertie G du solide S. Le graphe obtenu est enregistré dans le dossier physique, documents de travail, TS. Ouvrir le
document «oscillation élastique ».
II. DÉTERMINATION DES GRANDEURS CARACTÉRISTIQUES DE L'OSCILLATEUR
1) Obtention de x(t) à partir de u(t)
Le graphe obtenu est celui des variations de la tension UOA au cours du temps. On souhaite obtenir celui donnant les
variations de la position x du point G au cours du temps (attention, synchronie note T sa variable temps, ne pas
confondre cette grandeur avec une période).
 Sachant que la tension entre le point O et le point P1 (à droite) est de 6V, quelle relation numérique permet de
déterminer l’élongation x (en mètre) en fonction de u ? (on donne la distance OP1=5,5 cm).
 Utiliser la feuille de calcul pour créer cette variable x. Tracer en fenêtre 2 le graphe x(t)
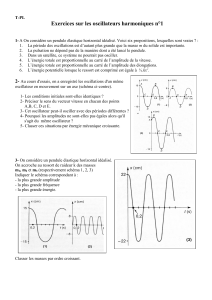
 Observer le graphe obtenu. Indiquer les caractéristiques du mouvement à l’instant t=0 (moment où on a déclenché
l’acquisition de synchronie).
2) Etude de x(t)
D'après le graphe :
 le solide S était-il soumis à des frottements au cours de ce mouvement? Justifier.
 Qualifier les oscillations du solide S.
 Déterminer la valeur de la pseudo-période To du mouvement (utiliser le réticule, puis origine relative).
 Vérifier que la pseudo-période reste la même au cours du temps.
 Le système {ressort+ solide S} est équivalent à un oscillateur élastique avec un seul ressort de raideur k, lié au
solide S. En déduire, par le calcul, une valeur de la constante k du ressort.
 Quelle est la première valeur de l’amplitude Xm enregistrée?
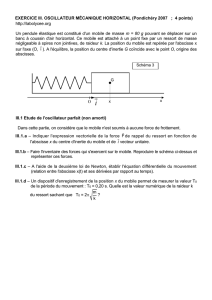
3) Tracé de vx(t)
 Quelle relation existe-t-il entre x(t) et vx(t) ?
 Créer la variable vx dans la feuille de calcul de synchronie.
 Tracer vx(t) sur la même fenêtre 2. Modifier l’échelle de la fenêtre ( 0.5 en ordonnée)
 Dans ces conditions x(t) est petite par rapport à vx(t) mais le graphe permet de comparer les 2 grandeurs.
Comparer la période de vx(t) à celle de x(t).
 Que fait x quand vx(t) est nulle? Est-ce cohérent avec l'expérience ? En quelle position vx(t) est-elle maximale ?
x
Go
O
P1
x
G
A

III. ETUDE DES ENERGIES DE L'OSCILLATEUR AU COURS DU MOUVEMENT
1) Energies de l'oscillateur (=ensemble ressort+solideS)
L’oscillateur {ressort + solide S} possèdent divers types d’énergie : l’énergie cinétique Ec, l’énergie potentielle de
pesanteur Epp et l’énergie potentiel élastique Epe. La somme de ces 3 énergies est l’énergie mécanique Em.
a)Energie potentielle de pesanteur Epp(du ressort et de S)
Rappel : On définit un axe O'z des altitudes, vertical, orienté vers le haut. On choisit de prendre l'énergie
potentielle de pesanteur nulle en O’. Dans ces conditions l'énergie potentielle de pesanteur pour un solide de
masse m dont le centre d'inertie G est à l'altitude z est : Epp=mgz
 Dans le cas de cet oscillateur, on choisit le point origine des altitudes en G0. Quelle est donc la valeur de Epp
quand le système est dans sa position d'équilibre ?
 Que devient l'altitude du système au cours du mouvement? En déduire la valeur de Epp quel que soit t.
b) Energie cinétiqueEc
Rappel : Pour un solide S, de masse m et dont la valeur de la vitesse est v à la date t : Ec(t) =
2
1.
2mv
Pour l'oscillateur, on admet que l'énergie cinétique est essentiellement celle de S (autrement dit on néglige celle du
ressort).
 Quelle relation y-a-t-il entre v et vx ?
 Utiliser la feuille de calcul pour créer puis calculer la variable Ec. Tracer en fenêtre 3 l’évolution de cette énergie
en fonction du temps.
c) Energie potentielle élastique du ressort Epe
C'est l'énergie que le ressort possède dès qu'il est déformé : Epe=
2
1.
2kx
avec x l’élongation du ressort à la date
t.
 Utiliser la feuille de calcul pour créer puis calculer la variable Epe. Tracer en fenêtre 3 l’évolution de cette énergie
en fonction du temps.
d)Energie mécanique
 Utiliser la feuille de calcul pour créer puis calculer la variable Em. Tracer en fenêtre 3 l’évolution de cette énergie
en fonction du temps.
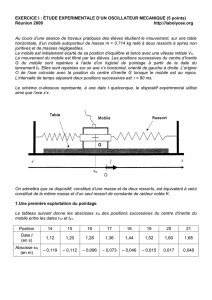
2) Interprétation des graphes obtenus
a) Mesurer la pseudo période T’ des énergies Ec(t) et Epe(t). La comparer à To.
b) Que devient Ec quand Epe est maximale et inversement ?
c) Que devient l'énergie mécanique au cours du temps ? Comment peut-on l'expliquer?
IV. MODELISATION D’UN OSCILLATEUR NON AMORTI
On souhaite modéliser un oscillateur non amorti ayant les mêmes propriétés que le précédent (même élongation
maximale et même période To). On appelle xh l’élongation de cette oscillateur non amorti.
 Donner l'expression de xh(t)en fonction de Xm,T0 et t (on rappelle que pour synchronie le temps t est T).
 Utiliser la feuille de calcul pour créer xh (sous le calcul de x) puis faire tracer la courbe xh(t) sur la fenêtre 2.
 Faire tracer la vitesse et les énergies (Il suffit de remplacer x par xh dans les formules de la feuille de calcul).
 Que peut-on dire de l'énergie mécanique d'un oscillateur élastique non amorti ?
 Retrouver ce résultat par une étude analytique : exprimer l'énergie mécanique à la date t en fonction de Xm, To,
m, k, connaissant l'expression de xh(t)

II. DETERMINATION DES GRANDEURS CARACTERISTIQUES DE L’OSCILLATEUR
1) Obtention de x(t) à partir de u(t)
x=U*0.055/6.
A l’instant t=0 (moment où on a déclenché l’acquisition), le solide était en x=0 et possédait une vitesse positive (x
croit au cours du temps donc
0
x
vx
)
2) Etude de x(t)
Le solide oscille sans apport d’énergie extérieure : les oscillations sont libres.
L’amplitudes xm des oscillations diminue au cours du temps, on a donc des oscillations amorties.
Conclusions : les oscillations sont libres et amorties.
To=562 ms sur la 1ère pseudo période
To=559 ms sur la 2ème To=562 ms sur la 3ème To=562 ms sur la 4ème
To reste sensiblement constant. Pour un solide S de masse m suspendue à un ressort de raideur k, la période est
donnée par la relation :
2
om
Tk
En prenant To=0,562 s, m=0,125 kg, on en déduit
4² ²
o
m
kT
=15,6 N.m-1
Amplitude Xm=37,2 mm=3,72 cm
3) Tracé de vx(t)
On a la vitesse
xdx
vx
dt
, qui s’écrit dans la feuille de calcul de synchronie par vx=deriv(x,T)
vx et x sont de mêmes périodes. Quand x est nulle, vx est maximale et inversement. Expérimentale, cela traduit bien
les fait suivants :
- la vitesse du centre d’inertie G est maximale quand il repasse par sa position d’équilibre
- la vitesse du centre d’inertie G est nulle quand le solide atteint son une élongation x=Xm
III. ETUDE DES ENERGIES DE L’OSCILLATEUR AU COURS DU MOUVEMENT
1) Energie de l’oscillateur
a) Energie potentielle de pesanteur
La position sur l’axe des altitudes du centre d’inertie étant repéré par z, l’énergie potentielle de pesanteur s’écrit
Epp=m.g.z. Go étant l’origine des altitudes, on a donc z(Go=0) et Epp=0.
Le mouvement étant horizontal, G reste à la même altitude que Go donc z(G)=0 et Epp reste nulle au cours du
mouvement : Epp(t)=0.
b) Energie cinétique
La vitesse du solide correspond à la valeur absolue de Vx :
x
vv
. On a donc v²=
x
v
²=
2
x
v
et Ec=
2
1.
2x
mv
2) Interprétation des graphes obtenus
On mesure la pseudo période des énergies :
Pour Ec (on mesure la pseudo période T’ entre deux valeurs nulles) : T’=286 ms
Pour Epe : même période T’=286 ms
On note donc que T’=To/2
L’énergie mécanique décroit au cours du temps, elle ne garde pas une valeur constante en raison des forces de
frottement sur le banc à coussin d’air.
IV. MODELISATION D’UN OSCILLATEUR AMORTI.
xh=Xm.cos (t+ ) avec Xm=3,72 cm=0,0372 m et = -  /2
xh=Xm.cos (t -  /2) = Xm. sin (t) où
2
o
T
=11,18 rad.s-1
Dans la feuille de calcul de synchronie, on utilise donc la formule xh=0.0372*sin(11.18*T)