Trigonométrie dans le triangle rectangle

Trigonométrie Page 1
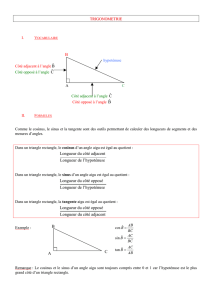
Trigonométrie dans le triangle rectangle.
Théorème de Pythagore
|BC|² =|AB|² + |AC|²
Distinguons les côtés du triangle,
 nous avons déjà l’hypoténuse qui est le côté opposé à l’angle droit et qui est le plus grand
côté.
Choisissons un angle de référence par exemple celui au sommet C
 [AC] est le côté de l’angle droit qui est adjacent à cet angle,
nous l’appellerons le côté adjacent à l’angle
C
ˆ
 [AB] est le côté de l’angle droit qui est opposé à cet angle,
nous l’appellerons le côté opposé à l’angle
C
ˆ
.
Exercice :
Dans chaque triangle
Colorie au crayon l’angle de 60°
Trace en rouge l’hypoténuse
Trace en vert le côté adjacent à l’angle de 60°
Trace en bleu le côté opposé à l’angle de 60°
« Dessiner ici quelques triangles rectangles ayant un angle de 60° »

Trigonométrie Page 2
Voici une figure que nous avons déjà rencontrée
lors de l’étude des triangles semblables
Les 3 triangles ABC, ABH et ACH sont
semblables car ils ont des angles égaux 2 à 2.
Calculons des rapports entre les longueurs des
côtés d’un même triangle.
Distinguons les côtés du triangle,
 nous avons déjà l’hypoténuse qui est le côté opposé à l’angle droit et qui est le plus grand
côté.
Choisissons un angle de référence par exemple celui au sommet C
 [AC] est le côté de l’angle droit qui est adjacent à cet angle,
nous l’appellerons le côté adjacent à l’angle
C
ˆ
 [AB] est le côté de l’angle droit qui est opposé à cet angle,
nous l’appellerons le côté opposé à l’angle
C
ˆ
.
Pour l’angle
C
ˆ
triangles
angle
droit
en
hypoténuse
côté
adjacent
à
C
ˆ
côté
opposé à
C
ˆ
adjacent
hypo
opposé
hypo
opposé
adjacent
ABC
A
BC=5
AC=3
AB=4
3/5
4/5
4/3
ABH
H
AB=4
ACH
H
AC=3
Nous constatons que le rapport
adjacent
hypo
est le même quel que soit le triangle rectangle semblable,
nous comprenons qu’il dépend bien de l’amplitude de l’angle
C
ˆ
nous baptiserons ce rapport : cosinus de l’angle
C
ˆ
, il est noté cos
C
ˆ
=
adjacent
hypo
nous pouvons dire de même pour
opposé
hypo
baptisé sinus de l’angle
C
ˆ
noté sin
C
ˆ
=
opposé
hypo
opposé
adjacent
baptisé tangente de l’angle
C
ˆ
noté tg
C
ˆ
=
opposé
adjacent

Trigonométrie Page 3
Faisons de même pour l’angle
B
ˆ
triangles
angle
droit
en
hypoténuse
côté
adjacent
à
B
ˆ
côté
opposé à
B
ˆ
adjacent
hypo
opposé
hypo
opposé
adjacent
ABC
A
BC=5
AB=4
AC=3
4/5
3/5
3/4
ABH
H
AB=4
ACH
H
AC=3
Nous constatons que
adjacent
hypo
est le même quel que soit le triangle rectangle semblable,
nous comprenons qu’il dépend bien de l’amplitude de l’angle
B
ˆ
ce rapport a déjà été baptisé, c’est le cosinus de l’angle
B
ˆ
noté cos
B
ˆ
=
adjacent
hypo
nous pouvons dire de même pour
opposé
hypo
baptisé sinus de l’angle
B
ˆ
noté sin
B
ˆ
=
opposé
hypo
opposé
adjacent
baptisé tangente de l’angle
B
ˆ
noté tg
B
ˆ
=
opposé
adjacent
Remarque : Dans un triangle rectangle, le plus grand côté est toujours ……………………
Nous pouvons donc dire que
cos
B
ˆ
=
adjacent
hypo
est ………………………………………………
sin
B
ˆ
=
opposé
hypo
est ………………………………………..……..…

Trigonométrie Page 4
Retenons les définitions suivantes :
Dans un triangle rectangle
En mesurant sur le dessin ci-dessous, détermine les valeurs trigonométriques approchées de
55°
cos 55° =
..............
.........
.......... 
sin 55° =
..............
.........
.......... 
tg 55° =
..............
.........
.......... 
Vérifie sur ta calculatrice
cos 55° = sin 55° = tg 55° =
Exercice : fais de même pour un angle de 65°
.........................
ˆ
tan
.........................
ˆ
cos
.........................
ˆ
sin
adjacent
opposé
C
hypoténuse
adjacent
C
hypoténuse
opposé
C

Trigonométrie Page 5
Utilisation de la calculette
La calculette connaît les valeurs trigonométriques de tous les angles
Note les valeurs au 1/1000ème près par défaut de
cos 68°=… sin 34°=……… tg 81°=…….
Elle permet aussi de retrouver l’angle quand on connaît le
rapport.
on sait par exemple que
5
3
ˆ
cos  hupo
adj
C
signifie que à l’angle
C
ˆ
on associe le rapport 3/5
5
3
ˆcos
C
nous allons utiliser la fonction retour qui s’appelle
1
cos
. Au rapport 3/5 on associe l’angle
C
ˆ
5
3
ˆ1
cos
C
À la calculette
C
ˆ
=
5
3
cos 1
…………..En valeur arrondie au degré près
C
ˆ
= ………
De même le retour de la fonction sin sera sin-1
Et celui de la fonction tg sera tg-1
Si nous avions utilisé la formule
5
4
ˆ
sin  hypo
opposé
C
. Nous aurions
5
4
sin
ˆ1
C
……….
Si nous avions utilisé la formule
3
4
ˆ adjacent
opposé
Ctg
. Nous aurions
3
4
ˆ1
tgC
………..
Nous pourrions faire de même pour l’angle
B
ˆ
,
mais nous pouvons le calculer plus facilement avec la somme des 3 angles du triangle :
90°+
C
ˆ
+
B
ˆ
= 180°
Donc
Au verso :Calcule
B
ˆ
avec une des autres formules
.........................
ˆ
tan
.........................
ˆ
sin
.........................
ˆ
cos
adjacent
opposé
B
hypoténuse
opposé
B
hypoténuse
adjacent
B